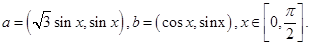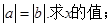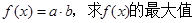题目内容
已知函数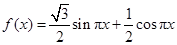 ,
, 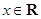 .
.
(1)求函数 的最大值和最小值;
的最大值和最小值;
(2)设函数 在
在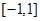 上的图象与
上的图象与 轴的交点从左到右分别为
轴的交点从左到右分别为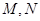 ,图象的最高点为
,图象的最高点为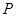 ,
,
求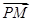 与
与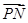 的夹角的余弦.
的夹角的余弦.
(1)1,-1;(2)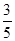 .
.
解析试题分析:(1)先利用两角和的正弦公式化简表达式,再求最大值和最小值;(2)通过解三角方程解出 的值,即得到
的值,即得到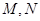 点的坐标,通过解方程
点的坐标,通过解方程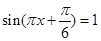 得到最高点的坐标,所以可以得到
得到最高点的坐标,所以可以得到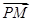 与
与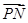 的坐标,再通过夹角公式求出夹角的余弦值.
的坐标,再通过夹角公式求出夹角的余弦值.
试题解析:(1)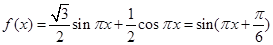 , 3分
, 3分
∵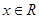 ,∴
,∴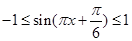 ,
,
∴函数 的最大值和最小值分别为1,-1. 5分
的最大值和最小值分别为1,-1. 5分
(2)解法1:令 得
得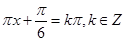 . 6分
. 6分
∵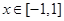 ,∴
,∴ 或
或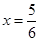 ,∴
,∴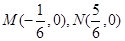 8分
8分
由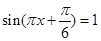 ,且
,且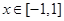 得
得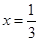 ,∴
,∴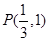 9分
9分
∴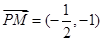 ,
,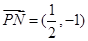 10分
10分
∴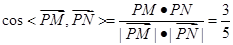 . 12分
. 12分
解法2:过点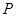 作
作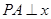 轴于
轴于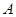 ,则
,则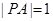 6分
6分
由三角函数的性质知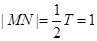 ,
, 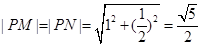 , 8分
, 8分
由余弦定理得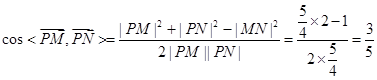 . 12分
. 12分
解法3:过点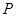 作
作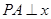 轴于
轴于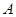 ,则
,则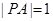 6分
6分
由三角函数的性质知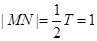 ,
,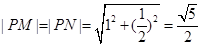 . 8分
. 8分
在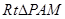 中,
中,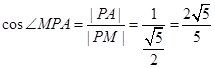 . 10分
. 10分
∵ 平分
平分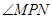 ,
,
∴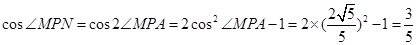 . 12分
. 12分
考点:1.两角和的正弦公式;2.解三角方程;3.夹角公式.

练习册系列答案
相关题目
 中,已知内角
中,已知内角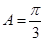 ,边
,边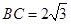 .设内角
.设内角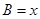 ,
, .
.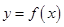 的解析式和定义域;
的解析式和定义域;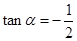 ,求
,求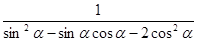 的值;
的值;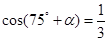 ,且
,且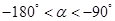 ,求
,求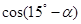 的值.
的值.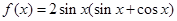 .
.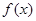 的最小正周期;
的最小正周期;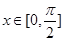 时,求
时,求 .
.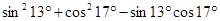 ;
;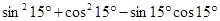 ;
; 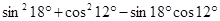 ;
;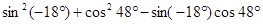 ;
;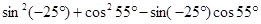 .
.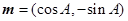 ,
,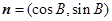 ,
,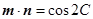 ,其中
,其中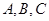 为
为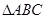 的内角.
的内角.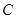 的大小;
的大小;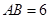 ,且
,且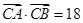 ,求
,求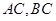 的长.
的长.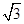 sinωxcosωx(ω>0)的最小正周期为π,
sinωxcosωx(ω>0)的最小正周期为π,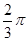 ]上的值域.
]上的值域.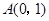 ,
,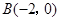 ,
,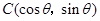 (
(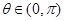 ),
),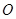 为坐标原点,向量
为坐标原点,向量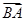 与向量
与向量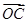 共线.
共线.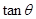 的值;
的值;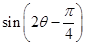 的值.
的值.