题目内容
给出下列四个命题:①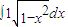 =
=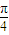 ,②α,β都是第三象限角,若cosα>cosβ,则sinα>sinβ,③对于两个变量之间的相关系数r,|r|≤1且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小;④设O为坐标原点,A(1,1),若点B满足
,②α,β都是第三象限角,若cosα>cosβ,则sinα>sinβ,③对于两个变量之间的相关系数r,|r|≤1且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小;④设O为坐标原点,A(1,1),若点B满足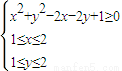 ,则
,则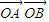 的最小值为2+
的最小值为2+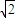 .其中正确的命题的个数是( )
.其中正确的命题的个数是( )A.0
B.1
C.2
D.3
【答案】分析:①根据定积分的几何意义可知正确;②根据三角函数线,当α,β都是第三象限角,若cosα>cosβ,则sinα<sinβ;③对于两个变量之间的相关系数的定义可知正确;④先根据点B(x,y)满足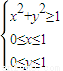 的平面区域,再把所求问题转化为求x+y的最小值,借助于线性规划知识即可求得结论.
的平面区域,再把所求问题转化为求x+y的最小值,借助于线性规划知识即可求得结论.
解答:解:①根据定积分的几何意义,表示以原点为圆心,1为半径在第一象限的面积,故正确;②根据三角函数线,当α,β都是第三象限角,若cosα>cosβ,则sinα<sinβ,故错误;③对于两个变量之间的相关系数的定义可知正确;④x2+y2-2x-2y+1≥0即(x-1)2+(y-1)2≥1,表示以(1,1)为圆心、以1为半径的圆周及其以外的区域.
当目标函数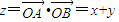 的图象同时经过目标区域上的点(1,2)、(2,1)时,目标函数
的图象同时经过目标区域上的点(1,2)、(2,1)时,目标函数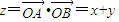 取最小值3,故错误.
取最小值3,故错误.
故选C.
点评:本题主要考查命题真假的判断,只有一一判断,是对基础知识的综合考查,属于基础题.
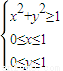 的平面区域,再把所求问题转化为求x+y的最小值,借助于线性规划知识即可求得结论.
的平面区域,再把所求问题转化为求x+y的最小值,借助于线性规划知识即可求得结论.解答:解:①根据定积分的几何意义,表示以原点为圆心,1为半径在第一象限的面积,故正确;②根据三角函数线,当α,β都是第三象限角,若cosα>cosβ,则sinα<sinβ,故错误;③对于两个变量之间的相关系数的定义可知正确;④x2+y2-2x-2y+1≥0即(x-1)2+(y-1)2≥1,表示以(1,1)为圆心、以1为半径的圆周及其以外的区域.
当目标函数
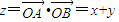 的图象同时经过目标区域上的点(1,2)、(2,1)时,目标函数
的图象同时经过目标区域上的点(1,2)、(2,1)时,目标函数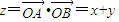 取最小值3,故错误.
取最小值3,故错误.故选C.
点评:本题主要考查命题真假的判断,只有一一判断,是对基础知识的综合考查,属于基础题.

练习册系列答案
相关题目