题目内容
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系![]() 的坐标平面
的坐标平面![]() 内,若函数
内,若函数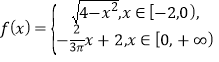 的图象与
的图象与![]() 轴围成一个封闭区域
轴围成一个封闭区域![]() ,将区域
,将区域![]() 沿
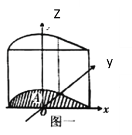
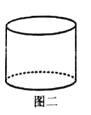
沿![]() 轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域![]() 面积相等,则此圆柱的体积为( )
面积相等,则此圆柱的体积为( )
A. ![]() B.
B. ![]() C. 2
C. 2![]() D.
D. ![]()
【答案】B
【解析】
求出函数![]() 的图象与
的图象与![]() 轴围成封闭区域
轴围成封闭区域![]() 的面积,再计算几何体的体积即可.
的面积,再计算几何体的体积即可.
由题意,函数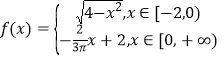 的图象
的图象
与![]() 轴围成一个封闭区域
轴围成一个封闭区域![]() 的面积为:
的面积为:
![]() ;
;
又几何体的高为![]() ,
,
![]() 所求几何体的体积为
所求几何体的体积为![]() ,
,
即此圆柱的体积为![]() .
.
故选:B

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
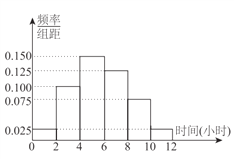
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”


