Question

【题目】在△ABC中，角A，B，C，所对的边分别为a，b，c．已知sinA+sinC=psinB（p∈R）．且ac= b2 ．
（Ⅰ）当p= ，b=1时，求a，c的值；
（Ⅱ）若角B为锐角，求p的取值范围．

Answer 1

【答案】（Ⅰ）解：由题设并利用正弦定理得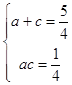
故可知a，c为方程x2﹣ x+ =0的两根，
进而求得a=1，c= 或a= ，c=1
（Ⅱ）解：由余弦定理得b2=a2+c2﹣2accosB=（a+c）2﹣2ac﹣2accosB=p2b2﹣ b2cosB﹣ ，
即p2= + cosB，
因为0＜cosB＜1，
所以p2∈（ ，2），由题设知p∈R，所以 ＜p＜ 或﹣ ＜p＜﹣
又由sinA+sinC=psinB知，p是正数
故 ＜p＜ 即为所求
【解析】（Ⅰ）利用正弦定理把题设等式中的角的正弦转化成边，解方程组求得a和c的值．（Ⅱ）先利用余弦定理求得a，b和c的关系，把题设等式代入表示出p2 ， 进而利用cosB的范围确定p2的范围，进而确定pd 范围．