题目内容
设{an}是公比不为1的等比数列，其前n项和为Sn，且a5，a3，a4成等差数列．
(1)求数列{an}的公比；
(2)证明：对任意k∈N*，Sk＋2，Sk，Sk＋1成等差数列．
（1）q＝－2（2）见解析
【解析】(1)设数列{an}的公比为q(q≠0，q≠1)，
由a5，a3，a4成等差数列，得2a3＝a5＋a4，
即2a1q2＝a1q4＋a1q3，
由a1≠0，q≠0得q2＋q－2＝0，解得q＝－2或1(舍去)，所以q＝－2.
(2)法一 对任意k∈N*，
Sk＋2＋Sk＋1－2Sk＝(Sk＋2－Sk)＋(Sk＋1－Sk)
＝ak＋1＋ak＋2＋ak＋1
＝2ak＋1＋ak＋1·(－2)＝0，
所以，对任意k∈N*，Sk＋2，Sk，Sk＋1成等差数列．
法二：对任意k∈N*,2Sk＝
，
Sk＋2＋Sk＋1＝
＋
＝
，
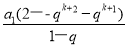2Sk－(Sk＋2＋Sk＋1)＝－
＝
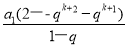
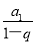[2(1－qk)－(2－qk＋2－qk＋1)]＝
(q2＋q－2)＝0，
因此，对任意k∈N*，Sk＋2，Sk，Sk＋1成等差数列．
练习册系列答案
相关题目
