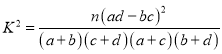题目内容
【题目】设![]() (e为自然对数的底数),
(e为自然对数的底数),![]() .
.
(I)记![]() ,讨论函
,讨论函![]() 单调性;
单调性;
(II)令![]() ,若函数G(x)有两个零点.
,若函数G(x)有两个零点.
(i)求参数a的取值范围;
(ii)设![]() 的两个零点,证明
的两个零点,证明![]() .
.
【答案】(Ⅰ)见解析; (Ⅱ)(i)a>0; (ii)见解析
【解析】
(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)(i)求出函数的导数,通过讨论a的范围,根据函数的零点的个数,求出a的范围即可;
(ii)根据a的范围,得到![]() ,令m>0,得到F (-1+m)﹣F(﹣1﹣m)
,令m>0,得到F (-1+m)﹣F(﹣1﹣m)![]() (
(![]() e2m+1),再令φ(m)
e2m+1),再令φ(m)![]() e2m+1,根据函数的单调性证明即可.
e2m+1,根据函数的单调性证明即可.
(Ⅰ)![]()
![]()
![]() ,
,
![]() ,所以
,所以
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
(Ⅱ)由已知,![]() ,
,
![]() .
.
![]() ①当
①当![]() 时,
时,![]() ,有唯一零点
,有唯一零点![]() ;
;
②当![]() 时,
时,![]() ,所以
,所以
当![]() 时,
时,![]() ,
,![]() 减;
减;
当![]() 时,
时,![]() ,
,![]() 增.
增.
所以![]() ,
,
因![]() ,所以当
,所以当![]() 时,
时,![]() 有唯一零点;
有唯一零点;
当![]() 时,
时,![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以,![]() ,
,![]() ,且
,且![]() ,当
,当![]() ,
,![]() 时,使
时,使![]() ,
,
取![]() ,则
,则![]() ,从而可知
,从而可知
当![]() 时,
时,![]() 有唯一零点,
有唯一零点,
即当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
③当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() ,或
,或![]() .
.
![]() 若
若![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 是单调减函数,至多有一个零点;
是单调减函数,至多有一个零点;
![]() 若
若![]() ,即
,即![]() 时,
时,![]() ,注意到
,注意到![]() ,
,![]() 都是增函数,所以
都是增函数,所以
当![]() 时,
时,![]() ,
,![]() 是单调减函数;
是单调减函数;
当![]() 时,
时,![]() ,
,![]() 是单调增函数;
是单调增函数;
当![]() 时,
时,![]() ,
,![]() 是单调减函数.
是单调减函数.
又因为![]() ,所以
,所以
至多有一个零点;
![]() 若
若![]() ,即
,即![]() 时,同理可得
时,同理可得
当![]() 时,
时,![]() ,
,![]() 是单调减函数;
是单调减函数;
当![]() 时,
时,![]() ,
,![]() 是单调增函数;
是单调增函数;
当![]() 时,
时,![]() ,
,![]() 是单调减函数.
是单调减函数.
又因为![]() ,所以
,所以![]() 至多有一个零点.
至多有一个零点.
综上,若函数![]() 有两个零点,则参数
有两个零点,则参数![]() 的取值范围是
的取值范围是![]() .
.
![]() 由
由![]() 知,函数
知,函数![]() 有两个零点,则参数
有两个零点,则参数![]() 的取值范围是
的取值范围是![]() .
.
![]() ,
,![]() 是
是![]() 的两个零点,则有
的两个零点,则有
 ,
,
因![]() ,则
,则![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由(Ⅰ)知,当![]() 时,
时,![]() 是减函数;当
是减函数;当![]() 时,
时,![]() 是增函数.
是增函数.
令![]() ,
,![]() ,
,
再令φ(m)![]() e2m+1=e2m
e2m+1=e2m![]() 1,,
1,,
![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以
![]() 时,
时,![]() 恒成立,即
恒成立,即
![]() 恒成立,
恒成立,
令![]() ,即
,即![]() ,有
,有![]() ,即
,即
![]() ,
,
因为![]() ,所以
,所以![]() ,又
,又![]() ,必有
,必有![]() ,
,
又当![]() 时,
时,![]() 是增函数,所以
是增函数,所以![]() ,即
,即
![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?
(3)若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
参考公式:

![]()
其中![]() 。临界值表:
。临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据:![]()
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是( )
.下列结论正确的是( )
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关