题目内容

19．设U为全集，A、B是U的子集，则“存在集合C使得A⊆C，B⊆∁UC”是“A∩B=ϕ”的充要条件条件．（选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”）

分析 根据充分条件和必要条件的定义结合集合关系进行判断即可．

解答 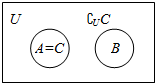解：若存在集合C使得A⊆C，B⊆∁UC，则可以推出A∩B=∅；
若A∩B=∅，由Venn图（如图）可知，
存在A=C，同时满足A⊆C，B⊆∁UC．
故“存在集合C使得A⊆C，B⊆∁UC”是“A∩B=∅”的充要条件．
故答案为：充要条件

点评 本题主要考查充分条件和必要条件的判断，根据集合关系是解决本题的关键．

练习册系列答案
相关题目
9．已知集合A={x|x2-2x-3≤0}，B={x|-2≤x＜2}，则A∪B=（　　）
A．[-2，3]B．[-3，2]C．[-1，2]D．[-1，2）
10．已知（$\sqrt{x}$-$\frac{1}{2\root{4}{x}}$）n展开式中第5项是常数项．
（1）求n的值；
（2）求展开式中所有有理项．
7．已知sin（$\frac{π}{3}$-α）=$\frac{3}{5}$，则cos（$α+\frac{π}{6}$）=$\frac{3}{5}$．
14．已知集合A={x|x2-3x+2≤0}，集合B为函数y=x2-2x+a的值域，集合C={x|（x-a）[x-（a+4）≤0]}．
（1）若A∩B=∅，求实数a的取值范围；
（2）若A∪C=C，求实数a的取值范围．
4．方程$\frac{x|x|}{4}$+y|y|=-1确定的曲线即为y=f（x）的图象，对于函数f（x）有如下结论：
①f（x）单调递增；
②函数g（x）=2f（x）+x不存在零点；
③f（x）的图象与h（x）的图象关于原点对称，则h（x）的图象就是方程$\frac{y|y|}{4}$+x|x|=1确定的曲线；
④f（x）的图象上的点到原点的最小距离为1．
则上述结论正确的是②④（只填序号）
11．不论a为何实数，直线ax+y+1=0与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{m}$=1总有公共点，则实数m的取值范围是[1，4）∪（4，+∞）．
8．已知数列{an}中，an=2an-1+n（n＞1，n∈N*）．
（1）若a1=1，求a2，a3，a4；
（2）若{an}为等差数列，求{an}的通项公式；
（3）{an}能否为等比数列？若是，求其通项公式；若不是，请说明理由．
9．在△ABC中，角A，B，C所对的边分别为a，b，c，已知b2-2c2-bc=0，a=$\sqrt{6}$，cosA=$\frac{7}{8}$，则△ABC的面积S为（　　）
A．$\frac{8\sqrt{15}}{5}$B．$\sqrt{15}$C．$\frac{\sqrt{15}}{2}$D．6$\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网