题目内容
【题目】已知方程![]() 的曲线是圆C,
的曲线是圆C,
(1)若直线l:![]() 与圆C相交于M、N两点,且
与圆C相交于M、N两点,且![]() (O为坐标原点),求实数m的值;
(O为坐标原点),求实数m的值;
(2)当![]() 时,设T为直线n:
时,设T为直线n:![]() 上的动点,过T作圆C的两条切线TG、TH,切点分别为G、H,求四边形TGCH而积的最小值.
上的动点,过T作圆C的两条切线TG、TH,切点分别为G、H,求四边形TGCH而积的最小值.
【答案】(1)![]()
(2)2
【解析】
(1)设![]() ,
,![]() ,则
,则![]()
![]() ,进一步得到
,进一步得到![]() ,联立直线方程与圆的方程,化为关于y的一元二次方程,利用韦达定理结合
,联立直线方程与圆的方程,化为关于y的一元二次方程,利用韦达定理结合![]() 即可求得实数
即可求得实数![]() 的值;
的值;
(2)当![]() 时,圆
时,圆![]() 的方程为
的方程为![]() ,求出圆心坐标与半径,由于
,求出圆心坐标与半径,由于![]() 为圆
为圆![]() 的两条切线,可得
的两条切线,可得![]() .再求出点
.再求出点![]() 到直线
到直线![]() 的距离
的距离![]() ,即可求得答案.
,即可求得答案.
(1)解:设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
得![]() ,即
,即![]() .
.
因为![]() ,则得
,则得![]() ,所以
,所以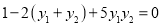 ①
①
联立![]() ,得
,得![]() .
.
由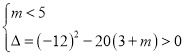 得
得![]() .
.
于是![]() ,
,![]() . 代入①得
. 代入①得![]() .
.
解得![]() ,符合题意.
,符合题意.
所以所求实数m的值等于![]() .
.
(2)当![]() 时,圆C的方程为
时,圆C的方程为![]() ,
,
即![]() ,所以圆C的圆心坐标是
,所以圆C的圆心坐标是![]() ,半径是1.
,半径是1.
由于TG、TH为C的两条切线,所以![]() .
.
又![]() ,而
,而![]() 的最小值为点C到直线n的距离d.
的最小值为点C到直线n的距离d.
![]() ,
,![]()
因此四边形TGCH面积的最小值是2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目