题目内容
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE= ![]() BC,PB⊥AE.
BC,PB⊥AE. 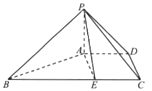
(1)求证:AB⊥PE;
(2)求二面角B﹣PC﹣D的余弦值.
【答案】
(1)证明:∵PA⊥平面ABCD,AE平面ABCD,
∴PA⊥AE,
又∵PB⊥AE,PB∩PA=P,
∴AE⊥平面PAB,又∵AB平面PAB,
∴AE⊥AB.
又∵PA⊥AB,PA∩AE=A,
∴AB⊥平面PAE,
又∵PE平面PAE,
∴AB⊥PE.
(2)解:以A为坐标原点,建立如图所示的空间直角坐标系A﹣xyz,
则B(2 ![]() ,0,0),P(0,0,2),C(﹣
,0,0),P(0,0,2),C(﹣ ![]() ,3,0),D(﹣
,3,0),D(﹣ ![]() ,1,0),
,1,0),
∴ ![]() =(﹣3
=(﹣3 ![]() ,3,0),
,3,0), ![]() =(﹣
=(﹣ ![]() ,3,﹣2),
,3,﹣2), ![]() =(0,2,0).
=(0,2,0).
设平面PBC的一个法向量 ![]() =(x,y,z),
=(x,y,z),
则 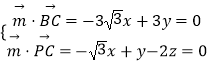 ,令x=1,得
,令x=1,得 ![]() =(1,
=(1, ![]() ,
, ![]() ).
).
同理可求平面PCD的一个法向量 ![]() =(2,0,﹣
=(2,0,﹣ ![]() ).
).
∴cos ![]() >=
>= ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∵二面角B﹣PC﹣D为钝二面角,
∴二面角B﹣PC﹣D的余弦值为﹣ ![]() .
.
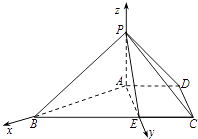
【解析】(1)推导出PA⊥AE,AE⊥AB.由此能证明AB⊥PE.(2)以A为坐标原点,建立空间直角坐标系A﹣xyz,利用向量法能求出二面角B﹣PC﹣D的余弦值.
【考点精析】根据题目的已知条件,利用棱锥的结构特征的相关知识可以得到问题的答案,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目