Question

【题目】已知直线：，若存在实数使得一条曲线与直线有两个不同的交点，且以这两个交点为端点的线段长度恰好等于，则称此曲线为直线的“绝对曲线”.下面给出的四条曲线方程：

①；②；③；④.

其中直线的“绝对曲线”的条数为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

由y=ax+1﹣a=a（x﹣1）+1，可知直线l过点A（1，1）．

对于①，y=﹣2|x﹣1|，图象是顶点为（1，0）的倒V型，而直线l过顶点A（1，1）．所以直线l不会与曲线y=﹣2|x﹣1|有两个交点，不是直线l的“绝对曲线”；

对于②，（x﹣1）2+（y﹣1）2=1是以A为圆心，半径为1的圆，

所以直线l与圆总有两个交点，且距离为直径2，所以存在a=±2，使得圆（x﹣1）2+（y﹣1）2=1与直线l有两个不同的交点，且以这两个交点为端点的线段的长度恰好等于|a|．

所以圆（x﹣1）2+（y﹣1）2=1是直线l的“绝对曲线”；

对于③，将y=ax+1﹣a代入x2+3y2=4，

得（3a2+1）x2+6a（1﹣a）x+3（1﹣a）2﹣4=0．

x1+x2=, x1x2=．

若直线l被椭圆截得的线段长度是|a|，

则

化简得．

令f（a）=．

f（1），f（3）．

所以函数f（a）在（1，3）上存在零点，即方程有根．

而直线过椭圆上的定点（1，1），当a∈（1，3）时满足直线与椭圆相交．

故曲线x2+3y2=4是直线的“绝对曲线”．

对于④将y=ax+1﹣a代入.

把直线y=ax+1-a代入y2=4x得a2x2+（2a-2a2-4）x+（1-a）2=0，
∴x1+x2=，x1x2=．
若直线l被椭圆截得的弦长是|a|，

则a2=（1+a2）[（x1+x2）2-4x1x2]=（1+a2）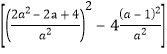

化为a6-16a2+16a-16=0，
令f（a）=a6-16a2+16a-16，而f（1）=-15<0，f（2）=16>0．
∴函数f（a）在区间（1，2）内有零点，即方程f（a）=0有实数根，当a∈（1，2）时，直线满足条件，即此函数的图象是“绝对曲线”．
综上可知：能满足题意的曲线有②③④．
故选：C．