题目内容
已知集合M={x|-x2+3x+28≥0}，N={x|x2-x-6＞0}，则M∩N为（ ）
| A．{x|-4≤x＜-2或3＜x≤7} | B．{x|x≤-2或x＞3} |
| C．{x|-4＜x≤-2或3≤x＜7} | D．{x|x＜-2或x≥3} |
∵-x2+3x+28≥0，∴（x-7）（x+4）≤0，解得-4≤x≤7，∴A=[-4，7]．
∵x2-x-6＞0，化为（x-3）（x+2）＞0，解得x＞3，或x＜-2．∴B={x|x＞3或x＜-2}．
∴A∩B=[-4，-2）∪（3，7]．
故选A．
∵x2-x-6＞0，化为（x-3）（x+2）＞0，解得x＞3，或x＜-2．∴B={x|x＞3或x＜-2}．
∴A∩B=[-4，-2）∪（3，7]．
故选A．
练习册系列答案
相关题目
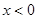使得不等式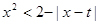
成立，则实数t的取值范围是 。
≤
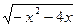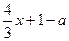的解集是[-4,0],则a的取值范围是（ ）
