题目内容
12.己知f(x)=ex-alnx-a,其中常数a>0.(1)当a=e时,求函数f(x)的极值;
(2)若函数y=f(x)有两个零点x1,x2(0<x1<x2),求证:$\frac{1}{a}<{x_1}<1<{x_2}$<a;
(3)求证:e2x-2-ex-1lnx-x≥0.
分析 (1)求出a=e的函数的导数,求出单调区间,即可求得极值;
(2)先证明:当f(x)≥0恒成立时,有 0<a≤e成立.若$0<x≤\frac{1}{e}$,则f(x)=ex-a(lnx+1)≥0显然成立;若$x>\frac{1}{e}$,运用参数分离,构造函数通过求导数,运用单调性,结合函数零点存在定理,即可得证;
(3)讨论当a=e时,显然成立,设$h(x)=\frac{x}{e^x}(x>0)$,求出导数,求出单调区间可得最大值,运用不等式的性质,即可得证.
解答 解:函数f(x)的定义域为(0,+∞),
(1)当a=e时,f(x)=ex-elnx-e,$f'(x)={e^x}-\frac{e}{x}$,
而$f'(x)={e^x}-\frac{e}{x}$在(0,+∞)上单调递增,又f′(1)=0,
当0<x<1时,f′(x)<f'(1)=0,则f(x)在(0,1)上单调递减;
当x>1时,f′(x)>f'(1)=0,则f(x)在(1,+∞)上单调递增,
则f(x)有极小值f(1)=0,没有极大值;
(2)先证明:当f(x)≥0恒成立时,有 0<a≤e成立.
若$0<x≤\frac{1}{e}$,则f(x)=ex-a(lnx+1)≥0显然成立;
若$x>\frac{1}{e}$,由f(x)≥0得$a≤\frac{e^x}{lnx+1}$,
令$φ(x)=\frac{e^x}{lnx+1}$,则$φ'(x)=\frac{{{e^x}(lnx+1-\frac{1}{x})}}{{{{(lnx+1)}^2}}}$,
令$g(x)=lnx+1-\frac{1}{x}(x>\frac{1}{e})$,
由$g'(x)=1+\frac{1}{x^2}>0$得g(x)在$(\frac{1}{e},+∞)$上单调递增,
又g(1)=0,所以φ′(x)在$(\frac{1}{e},1)$上为负,在(1,+∞)上为正,
因此φ(x)在$(\frac{1}{e},1)$上递减,在(1,+∞)上递增,即有φ(x)min=φ(1)=e,
从而0<a≤e.因而函数y=f(x)若有两个零点,则a>e,即有f(1)=e-a<0,
由f(a)=ea-alna-a(a>e)得f'(a)=ea-lna-2,
则$f''(a)={e^a}-\frac{1}{a}>{e^a}-\frac{1}{e}>e-\frac{1}{e}>0$,
则f′(a)=ea-lna-2在(e,+∞)上单调递增,
即有f′(a)>f'(e)=ee-3>e2-3>0,
则有f(a)=ea-alna-a在(e,+∞)上单调递增,
则f(a)>f(e)=ee-2e>e2-2e>0,则f(1)f(a)<0,则有1<x2<a;
由a>e得$f(\frac{1}{a})={e^{\frac{1}{a}}}-aln\frac{1}{a}-a={e^{\frac{1}{a}}}+alna-a>{e^{\frac{1}{a}}}+alne-a={e^{\frac{1}{a}}}>0$,则$f(1)f(\frac{1}{a})<0$,
所以$\frac{1}{a}<{x_1}<1$,综上得$\frac{1}{a}<{x_1}<1<{x_2}<a$.
(3)证明:由(2)知当a=e时,f(x)≥0恒成立,所以f(x)=ex-elnx-e≥0,
即f(x)=ex-elnx≥e,
设$h(x)=\frac{x}{e^x}(x>0)$,则$h'(x)=\frac{1-x}{e^x}$,
当0<x<1时,h′(x)>0,所以h(x)在(0,1)上单调递增;
当x>1时,h′(x)<0,所以h(x)在(1,+∞)上单调递减,
所以$h(x)=\frac{x}{e^x}(x>0)$的最大值为$h(1)=\frac{1}{e}$,即$\frac{x}{e^x}≤\frac{1}{e}$,因而$\frac{x}{{{e^{x-2}}}}≤e$,
所以$f(x)={e^x}-elnx≥e≥\frac{x}{{{e^{x-2}}}}$,即e2x-2-ex-1lnx-x≥0.
点评 本题考查导数的运用:求单调区间和极值、最值,主要考查函数的单调性的运用,以及不等式恒成立问题转化为求函数的最值问题,属于中档题和易错题.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | $\frac{3}{14}$ | B. | $\frac{5}{14}$ | C. | $\frac{3}{28}$ | D. | $\frac{5}{28}$ |
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
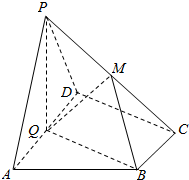 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$. 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC=BC,AB=2A1A=4.以AB,BC为邻边作平行四边形ABCD,连接A1D和DC1.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC=BC,AB=2A1A=4.以AB,BC为邻边作平行四边形ABCD,连接A1D和DC1.