题目内容
已知数列 满足:
满足: ,且
,且 ,
,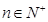 .
.
(1)求通项公式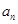 ;
;
(2)求数列的前n项的和
(1)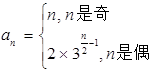 ;(2)
;(2) .
.
解析试题分析:(1)求通项公式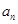 由已知
由已知 ,且
,且 ,
,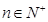 ,由于
,由于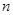 取奇数,与
取奇数,与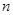 取偶数影响解析式,因此需对
取偶数影响解析式,因此需对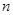 讨论,当
讨论,当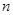 是奇数时,
是奇数时, ,得
,得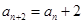 ,
,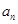 故数列
故数列 的奇数项
的奇数项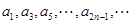 是等差数列,可求出通项公式,当
是等差数列,可求出通项公式,当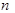 为偶数时,
为偶数时,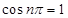 ,则
,则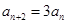 ,数列
,数列 的偶数项
的偶数项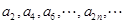 是等比数列,可求出通项公式,从而可得数列
是等比数列,可求出通项公式,从而可得数列 的通项公式
的通项公式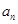 ;(2)求数列的前
;(2)求数列的前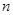 项的和
项的和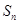 ,由(1)知数列
,由(1)知数列 的通项公式
的通项公式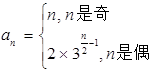 ,故它的前
,故它的前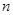 项的和
项的和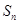 分情况求.
分情况求.
试题解析:(1)当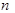 是奇数时,
是奇数时,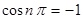 ,所以
,所以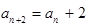 ,所以
,所以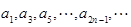 是首项为
是首项为 ,公差为2的等差数列,因此
,公差为2的等差数列,因此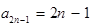 。 2分
。 2分
当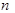 为偶数时,
为偶数时,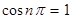 ,所以
,所以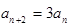 ,所以
,所以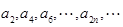 是首项为
是首项为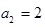 ,公比为3的等比数列,因此
,公比为3的等比数列,因此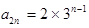 。 4分
。 4分
综上 6分
6分
(2)由(1)得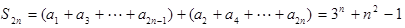 8分
8分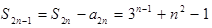 10分
10分
所以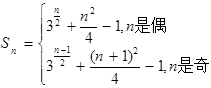 12分
12分
考点:数列的通项公式,求数列的前 项的和.
项的和.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
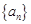 满足:
满足: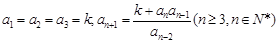 其中
其中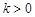 ,数列
,数列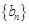 满足:
满足: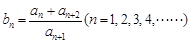
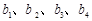 ;
;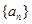 ,把
,把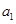 作为新数列
作为新数列 的第一项,把
的第一项,把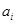 或
或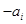 (
(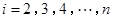 )作为新数列
)作为新数列 项,数列
项,数列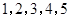 的一个生成数列是
的一个生成数列是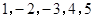 .已知数列
.已知数列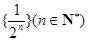 的生成数列,
的生成数列,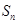 为数列
为数列 项和.
项和.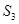 的所有可能值;
的所有可能值;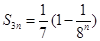 ,求数列
,求数列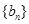 的通项公式;
的通项公式;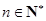 ,
,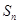 的所有可能值组成的集合为
的所有可能值组成的集合为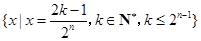 .
. 中,公比
中,公比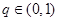 ,
, 且
且 和
和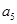 的等比中项是
的等比中项是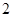 .
.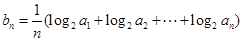 ,判断数列
,判断数列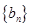 的前
的前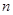 项和
项和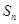 是否存在最大值,若存在,求出使
是否存在最大值,若存在,求出使 ,
,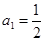 ,且满足
,且满足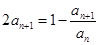 .
. 是等差数列;
是等差数列;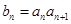 ,求数列
,求数列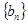 的前n项和
的前n项和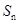 .
.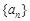 的首项
的首项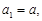 其中
其中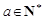 ,
,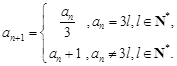 ,令集合
,令集合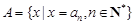 .
.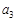 是数列
是数列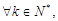 恒有
恒有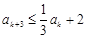 成立;
成立;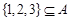 .
.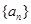 的前
的前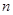 项和为
项和为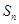 ,已知对任意的
,已知对任意的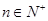 ,点
,点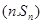 均在函数
均在函数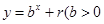 且
且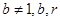 均为常数)的图像上.
均为常数)的图像上.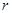 的值;
的值;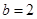 时,记
时,记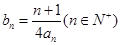 ,求数列
,求数列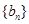 的前
的前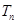 .
.