题目内容
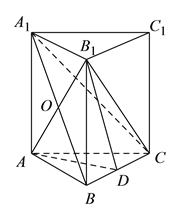
【题目】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() 与
与![]() 交于点
交于点![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求证: ![]() 平面
平面![]() .
.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?请说明理由.
?请说明理由.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)当![]() 为
为![]() 中点时,
中点时, ![]() .
.
【解析】试题分析:(Ⅰ)证明:连结OD,可证OD为△A1BC的中位线,可得OD∥A1C,即可判定A1C∥平面AB1D.(Ⅱ)在直三棱柱ABC-A1B1C1中,可证AC⊥平面AA1B1B,从而可得AC⊥A1B,又A1B⊥AB1,AC∩AB1=A,即可证明A1B⊥平面AB1C.(Ⅲ)取B1C中点E,连结DE,AE,可证DE⊥BC,AD⊥BC,从而证明BC⊥平面ADE,进而可证BC⊥AE,即可得解.
试题解析:
(Ⅰ)连接![]() ,∴
,∴![]() ,∴四边形
,∴四边形![]() 为正方形.∴
为正方形.∴![]() 为
为![]() 中点,又
中点,又![]() 为
为![]() 中点,∴
中点,∴![]() 为
为![]() 的中位线,∴
的中位线,∴![]() .∵
.∵![]() 平面
平面![]() ,
, ![]() 面
面![]() ,
,
∴![]() 面
面![]() .
.
(Ⅱ)由题知![]() ,
, ![]() ,又
,又![]() ,∴
,∴ ![]() 面
面![]() ,
,
∴![]() .在正方形
.在正方形![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() 面
面![]() .
.
(Ⅲ)存在,取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() .∴
.∴ ![]() ,∴
,∴ ![]() .
.
∵![]() ,
, ![]() 为
为![]() 中点,∴
中点,∴![]() .∵
.∵ ![]() ,∴
,∴ ![]() 面
面![]() ,
,
∴![]() ,∴当
,∴当![]() 为
为![]() 中点时,
中点时, ![]() .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 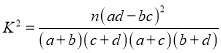 )
)