题目内容
(本小题满分12分)
在边长为2的正方体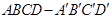 中,E是BC的中点,F是
中,E是BC的中点,F是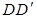 的中点
的中点
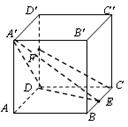
(1)求证:CF∥平面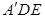
(2)求二面角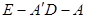 的平面角的余弦值.
的平面角的余弦值.
在边长为2的正方体
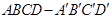 中,E是BC的中点,F是
中,E是BC的中点,F是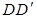 的中点
的中点
(1)求证:CF∥平面
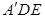
(2)求二面角
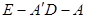 的平面角的余弦值.
的平面角的余弦值.(1)根据线面平行的判定定理,结合CF∥OE ,来得到证明。
(2)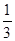
(2)
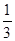
试题分析:解:(Ⅰ)取A’D的中点O,连接OF
∵点F为DD’的中点;
∴OF∥A’D’且OF=
 A’D’;
A’D’;∴OF∥AD且OF=
 AD; 2分
AD; 2分∵点E为BC的中点
∴EC∥AD且EC=
 AD;
AD;∴OF∥EC且OF=EC;
∴四边形OBCF为平行四边形 .3分
∴CF∥OE
又FC
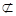 面A’DE且OE
面A’DE且OE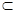 面A’DE
面A’DE∴CF∥面A’DE .6分
(Ⅱ)取AD的中点M,连接ME
过点M作MH⊥A’D,垂足为H点,连接HE
∵AB∥ME,又AB⊥面ADD’A’
∴ME⊥面ADD’A’
∵A’D
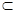 面ADD’A’
面ADD’A’∴ME⊥A’D
又ME⊥A’D,ME∩MH = M
∴A’D⊥面MHE
∵HE
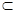 面MHE
面MHE∴A’D⊥HE
∴∠MHE是二面角E-A’D-A的平面角 .9分
在Rt△MHD中, sin∠A’DA =
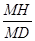
∴MH =" sin" 45°=
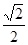
在Rt△MHD中,tan∠MHE =
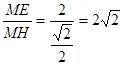
∴sin∠MHE =
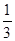 .12分
.12分点评:解决俄ud关键是对于线面平行的判定定理的运用,以及二面角的求解,属于基础题。

练习册系列答案
相关题目
 是平面
是平面 内的一条定直线,
内的一条定直线, 是平面
是平面 经过点
经过点 角,则直线
角,则直线 的轨迹是
的轨迹是 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, .
.

 ;
; ,求二面角
,求二面角 的余弦值.
的余弦值. ( )
( )



 是直线,
是直线, 是平面,给出下列命题:
是平面,给出下列命题: ,
, ,
, ,则
,则 或
或 .
. ,
, ,
, ,则
,则 .
.
 ,n
,n ,n∥
,n∥ 且
且 ,
, ,则
,则
 N
N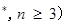 个平面,任意三个平面不经过同一条直线.若这
个平面,任意三个平面不经过同一条直线.若这 个平面将空间分成
个平面将空间分成 个部分,则
个部分,则 ,
, .
.  、
、 为两条不同的直线,
为两条不同的直线, 、
、 为两个不同的平面,则下列推理中正确的是( )
为两个不同的平面,则下列推理中正确的是( )




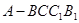 中,
中, 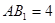 ,底面ABC是正三角形,
,底面ABC是正三角形,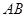 =2.四边形
=2.四边形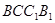 是矩形,二面角
是矩形,二面角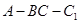 为直二面角,D为
为直二面角,D为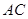 中点。
中点。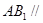 平面
平面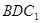 ;
;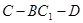 的余弦值.
的余弦值. 中,E为AC中点
中,E为AC中点

 ,
,