题目内容
1.有一项活动,需在3名教师,8名男生和5名女生中选人参加.(1)需一人参加,选到教师的概率是多少?
(2)需三人参加,选到一名教师、一名男生、一名女生的概率是多少?
(3)需三人参加,选到至少一名教师的概率是多少?
分析 (1)计算出在3名教师,8名男生和5名女生中选一人参加活动的方法总数,及选到教师的方法种数,代入古典概型概率计算公式,可得答案;
(2)计算出在3名教师,8名男生和5名女生中选三人参加活动的方法总数,及选到一名教师、一名男生、一名女生的方法种数,代入古典概型概率计算公式,可得答案;
(3)计算出在3名教师,8名男生和5名女生中选三人参加活动的方法总数,及选到至少一名教师的方法种数,代入古典概型概率计算公式,可得答案;
解答 解:(1)在3名教师,8名男生和5名女生中选一人参加活动,
共有3+8+5=16种不同的方法,
其中选到教师的方法有3种,
故选到教师的概率P=$\frac{3}{16}$;
(2)在3名教师,8名男生和5名女生中选三人参加活动,
共有${C}_{16}^{3}$=560种不同的方法,
其中选到一名教师、一名男生、一名女生的方法有:3×8×5=120种,
故选到一名教师、一名男生、一名女生的概率P=$\frac{120}{560}$=$\frac{3}{14}$,
(3)在3名教师,8名男生和5名女生中选三人参加活动,
共有${C}_{16}^{3}$=560种不同的方法,
其中没有选到教师的情况有${C}_{13}^{3}$=286种,
则选到至少一名教师的情况有560-286=274种,
故选到至少一名教师的概率P=$\frac{274}{560}$=$\frac{137}{280}$
点评 本题考查的知识点是古典概型概率计算公式,熟练掌握利用古典概型概率计算公式求概率的方法和步骤是解答的关键.

练习册系列答案
相关题目
9.已知向量$\vec a$=(1,n),$\vec b$=(-1,n),$\vec a$垂直于$\vec b$,则|${\vec a}$|=( )
| A. | 1 | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | 4 |
16.运行如图所示的程序框图,则输出k的值是( )
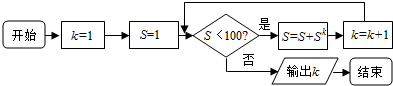

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13.有4部车床需加工3个不同的零件,不同的安排方法有多少种?( )
| A. | 34 | B. | 43 | C. | 13 | D. | 14 |
 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2$\sqrt{3}$,AC=2,
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2$\sqrt{3}$,AC=2,