题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上存在单调增区间,求实数
上存在单调增区间,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,证明:对于
,证明:对于![]() ,总有
,总有![]()
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)求出![]() 的导数,将其转化为在区间
的导数,将其转化为在区间![]() 内存在区间使得即
内存在区间使得即![]() 在
在![]() 上能成立,根据函数
上能成立,根据函数![]() 的最小值即可确定
的最小值即可确定![]() 的范围;(2)问题转化为证明
的范围;(2)问题转化为证明![]() ,在
,在![]() 上恒成立,构造函数
上恒成立,构造函数![]() ,
,![]() ,求出
,求出![]() 的导数,判断出函数的单调性,从而证出结论.
的导数,判断出函数的单调性,从而证出结论.
(1)由题![]() ,
,
因为函数![]() 在
在![]() 存在单调增区间,
存在单调增区间,
故在区间![]() 内存在区间使得
内存在区间使得![]() 成立,
成立,
即![]() 能成立,
能成立,
即![]() 在
在![]() 上能成立,
上能成立,
而![]() 在
在![]() 的最小值是
的最小值是![]() ,
,
故![]() ;
;
(2)若![]() ,则
,则![]() ,
,
![]() ,
,
而![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
要证原不等式成立,只要证![]() ,
,
只要证![]() ,
,
只要证![]() ,在
,在![]() 上恒成立,
上恒成立,
首先构造函数![]() ,
,![]() ,
,
因为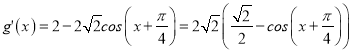 ,
,
可得,在![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是减函数,
上是减函数,
在![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是增函数,
上是增函数,
所以,在![]() 上,
上,![]() ,所以
,所以![]() ,
,
所以,![]() ,等号成立当且仅当
,等号成立当且仅当![]() 时,
时,
其次构造函数![]() ,
,![]() ,
,
因为![]() ,
,
可见![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是减函数,
上是减函数,
![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是增函数,
上是增函数,
所以在![]() 上,
上,![]() ,所以
,所以![]() ,
,
所以,![]() ,等号成立当且仅当
,等号成立当且仅当![]()
![]() 时.
时.
综上所述,![]() ,
,
因为取等条件并不一致,
所以![]() ,在
,在![]() 上恒成立,
上恒成立,
所以![]() ,总有
,总有![]() 成立.
成立.

练习册系列答案
相关题目
【题目】某工厂今年前5个月某种产品的产量(单位:万件)的数据如下表:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 4 | 6 | 6 |
(1)若从这5组数据中随机抽出2组,求抽出的2组数据恰好是不相邻两个月的数据的概率;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计今年6月份该种产品的产量.
,并估计今年6月份该种产品的产量.
参考公式: .
.