题目内容
设数列 、
、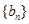 满足
满足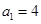 ,
,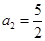 ,
,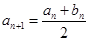 ,
,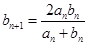 .
.
(1)证明: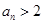 ,
,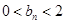 (
( );
);
(2)设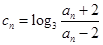 ,求数列
,求数列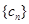 的通项公式;
的通项公式;
(3)设数列 的前
的前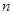 项和为
项和为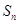 ,数列
,数列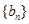 的前
的前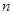 项和为
项和为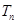 ,数列
,数列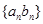 的前
的前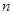 项和为
项和为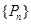 ,求证:
,求证: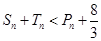 .
.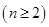
(1)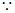
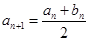 ,
,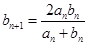 两式相乘得
两式相乘得 ,
,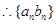 为常数列,
为常数列, ;
; 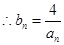

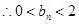 ;
;
(2)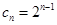 ;(3)由
;(3)由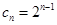 可以知道,
可以知道,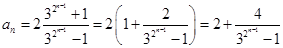 ,
,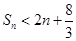 .又
.又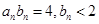 ,故
,故 ,
,
所以
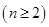 .
.
解析试题分析:(1)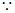
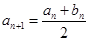 ,
,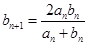 两式相乘得
两式相乘得 ,
,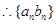 为常数列,
为常数列, ;(2分)
;(2分)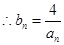

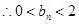 ;
;
(若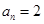 ,则
,则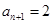 ,从而可得
,从而可得 为常数列与
为常数列与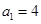 矛盾); 4分
矛盾); 4分
(2)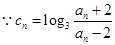 ,
,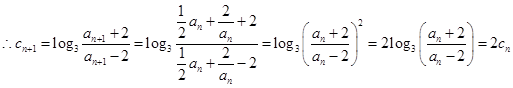
又因为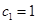 ,
, 为等比数列,
为等比数列, 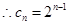 8分
8分
(3)由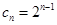 可以知道,
可以知道,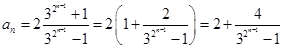 ,
,
令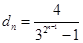 ,数列
,数列 的前
的前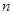 项和为
项和为 ,很显然只要证明
,很显然只要证明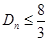
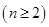 ,
,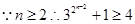 .
.
因为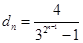
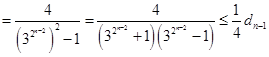 ,
,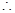
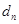
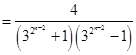
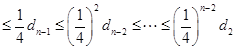
所以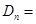


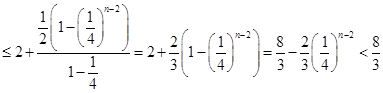
所以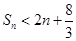 . 14分
. 14分
又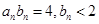 ,故
,故 ,
,
所以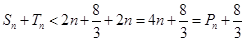
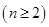 . 16分
. 16分
考点:数列与不等式的综合应用;数列通项公式的求法;数列前n项和的求法;数列的递推式。
点评:本题考查不等式的证明和数列的通项公式的求法,综合性强,难度大,是高考重点,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
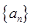 是等差数列,且满足:
是等差数列,且满足: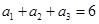 ,
,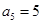 ;数列
;数列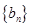 满足
满足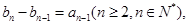
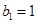 .
.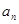 和
和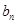 ;
;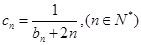 ,若
,若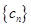 的前
的前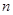 项和为
项和为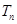 ,求证
,求证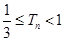 .
. 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:

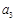 ……
…… 
 第1行
第1行
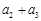 ……
…… 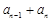 第2行
第2行 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
. ,求和
,求和 .
. 的前
的前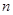 项和为
项和为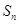 ,且
,且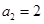 ,
,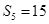 ,数列
,数列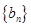 满足:
满足: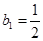 ,
, ,
,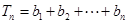 ,
,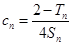 ,证明:
,证明:
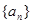 的前n项和为
的前n项和为 ,且
,且 ,(
,( =1,2,3…)
=1,2,3…)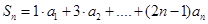 ,求
,求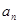 }的前项和为
}的前项和为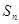 ,且
,且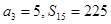 。数列
。数列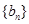 为等比数列,且首项
为等比数列,且首项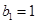 ,
,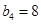 .
.  ,
,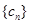 满足
满足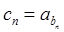 ,求数列
,求数列 项和为
项和为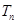 ;
;  为等差数列,且
为等差数列,且 ,
, .
. ,求证:数列
,求证:数列 是等比数列.
是等比数列.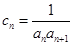 ,求数列
,求数列 的前
的前 项和
项和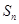 .
.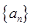 是首项为
是首项为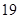 ,公差为
,公差为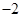 的等差数列,
的等差数列,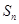 为
为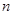 项和.
项和. 及
及 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前
的通项公式及其前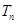 .
. 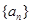 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且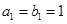 ,
,
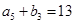 .
.  的前n项和
的前n项和 。
。