题目内容
已知数列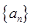 是等差数列,且满足:
是等差数列,且满足: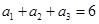 ,
,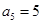 ;数列
;数列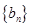 满足
满足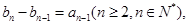
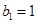 .
.
(1)求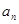 和
和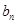 ;
;
(2)记数列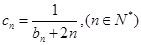 ,若
,若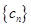 的前
的前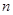 项和为
项和为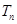 ,求证
,求证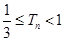 .
.
(1)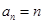 ;
; 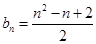 。(2)先求数列的和然后利用放缩法证明
。(2)先求数列的和然后利用放缩法证明
解析试题分析:(1)因为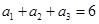 ,
,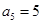 ,所以
,所以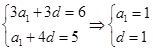 ,所以
,所以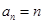 ;
;
又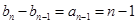 ,所以,
,所以,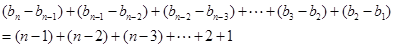
得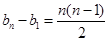 ,所以
,所以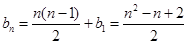 。
。
(2)因为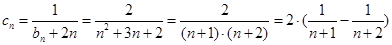 ,所以
,所以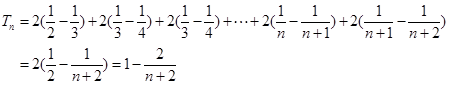
而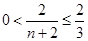 ,所以
,所以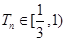 。
。
考点:本题考查了数列通项公式及前n项和
点评:数列的通项公式及应用是数列的重点内容,数列的大题对逻辑推理能力有较高的要求,在数列中突出考查学生的理性思维,这是近几年新课标高考对数列考查的一个亮点,也是一种趋势.随着新课标实施的深入,高考关注的重点为等差、等比数列的通项公式,错位相减法、裂项相消法等求数列的前n项的和等等

练习册系列答案
相关题目
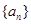 是公比大于
是公比大于 的等比数列,
的等比数列,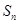 是
是 项和.若
项和.若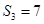 ,且
,且 ,
,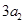 ,
, 构成等差数列.
构成等差数列.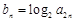 ,求数列
,求数列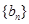 的前
的前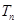 .
. 的前n项和为
的前n项和为 ,且满足
,且满足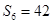 ,
,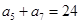 .
.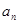 及前n项和
及前n项和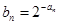 (
(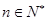 ),求数列
),求数列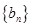 的前
的前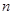 项和
项和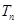 .
.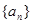 是等差数列,
是等差数列,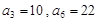 ,数列
,数列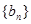 的前n项和是
的前n项和是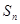 ,且
,且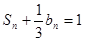 .
.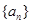 ,前
,前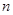 项和为
项和为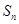 . 且满足
. 且满足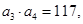
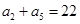 .
.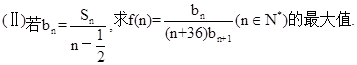
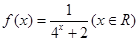 .
.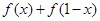 的值;
的值;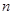 项和公式的推导方法,求:
项和公式的推导方法,求: 的值.
的值.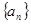 中,
中, ,
,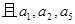 构成公比不等于1的等比数列.
构成公比不等于1的等比数列.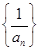 是等差数列;
是等差数列; 的值;
的值;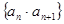 的前n项和为
的前n项和为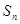 ,若对任意
,若对任意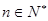 均有
均有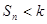 成立,求实数
成立,求实数 的范围.
的范围. 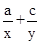 的值;
的值;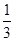 、c="-"
、c="-" 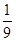 ,试计算
,试计算 、
、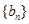 满足
满足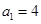 ,
,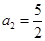 ,
,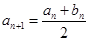 ,
,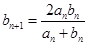 .
. 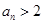 ,
,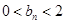 (
( );
);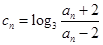 ,求数列
,求数列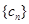 的通项公式;
的通项公式;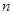 项和为
项和为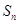 ,数列
,数列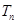 ,数列
,数列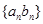 的前
的前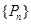 ,求证:
,求证: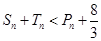 .
.