题目内容
过抛物线y2=4x的焦点的直线交抛物线于A、B两点,O为坐标原点,则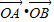 的值是( )
的值是( )A.3
B.-3
C.12
D.-12
【答案】分析:由抛物线y2=4x与过其焦点(1,0)的直线方程联立,消去y整理成关于x的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,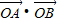 =x1•x2+y1•y2,由韦达定理可以求得答案.
=x1•x2+y1•y2,由韦达定理可以求得答案.
解答:解:由题意知,抛物线y2=4x的焦点坐标为(1,0),∴直线AB的方程为y=k(x-1),
由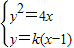 得k2x2-(2k2+4)x+k2=0,设A(x1,y1),B(x2,y2),
得k2x2-(2k2+4)x+k2=0,设A(x1,y1),B(x2,y2),
则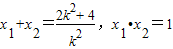 ,y1•y2=k(x1-1)•k(x2-1)=k2[x1•x2-(x1+x2)+1]
,y1•y2=k(x1-1)•k(x2-1)=k2[x1•x2-(x1+x2)+1]
∴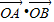 =x1•x2+y1•y2=
=x1•x2+y1•y2=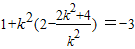 ,
,
从而排除A、C、D;
故选B.
点评:本题考查直线与圆锥曲线的关系,解决问题的关键是联立抛物线方程与过其焦点的直线方程,利用韦达定理予以解决,属于基础题.
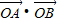 =x1•x2+y1•y2,由韦达定理可以求得答案.
=x1•x2+y1•y2,由韦达定理可以求得答案.解答:解:由题意知,抛物线y2=4x的焦点坐标为(1,0),∴直线AB的方程为y=k(x-1),
由
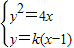 得k2x2-(2k2+4)x+k2=0,设A(x1,y1),B(x2,y2),
得k2x2-(2k2+4)x+k2=0,设A(x1,y1),B(x2,y2),则
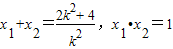 ,y1•y2=k(x1-1)•k(x2-1)=k2[x1•x2-(x1+x2)+1]
,y1•y2=k(x1-1)•k(x2-1)=k2[x1•x2-(x1+x2)+1]∴
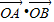 =x1•x2+y1•y2=
=x1•x2+y1•y2=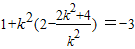 ,
,从而排除A、C、D;
故选B.
点评:本题考查直线与圆锥曲线的关系,解决问题的关键是联立抛物线方程与过其焦点的直线方程,利用韦达定理予以解决,属于基础题.

练习册系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A,B两点,则|AB|=( )
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则△AOB的面积为( )
| A、5 | ||
B、
| ||
C、
| ||
D、
|