题目内容
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线 的一部分,栏栅与矩形区域的边界交于点
的一部分,栏栅与矩形区域的边界交于点 ,交曲线于点
,交曲线于点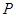 ,设
,设 .
.
(1)将△ (
( 为坐标原点)的面积
为坐标原点)的面积 表示成
表示成 的函数
的函数 ;
;
(2)若在 处,
处, 取得最小值,求此时
取得最小值,求此时 的值及
的值及 的最小值.
的最小值.
(1) ,(2)
,(2) .
.
解析试题分析:(1)求 的导函数,设出
的导函数,设出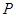 的坐标,确定过点
的坐标,确定过点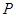 的切线方程,进而可得
的切线方程,进而可得 的坐标,表示出三角形的面积;(2)把
的坐标,表示出三角形的面积;(2)把 代入
代入 ,利用导数研究
,利用导数研究 的最值问题,即可确定△
的最值问题,即可确定△ (
( 为坐标原点)的面积的最小值.
为坐标原点)的面积的最小值.
试题解析:(1)∵曲线 ,可得
,可得 ,
, .
.
直线 的斜率为:
的斜率为: ,可得
,可得 ,
,
令 ,可得
,可得 ,可得
,可得 ;
;
令 ,可得
,可得 ,可得
,可得 ,
,
∴ ;
;
(2) 时,
时, 取得最小值,
取得最小值, ,
,
∴ ,可得
,可得 ,可得
,可得 ,
,
此时可得 的最小值为
的最小值为 .
.
考点:1.函数的最值;2.抛物线的应用;3.函数的解析式.

练习册系列答案
相关题目
 ,其中
,其中 是实数,设
是实数,设 为该函数的图象上的两点,且
为该函数的图象上的两点,且 .
. 的单调区间;
的单调区间; 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求 的最小值;
的最小值; ,
, 是定义域为R的奇函数,
是定义域为R的奇函数, ,
, 的值;
的值; 在x∈[2,3]上恒成立,求
在x∈[2,3]上恒成立,求 的取值范围.
的取值范围. .
. 时,函数
时,函数 恒有意义,求实数a的取值范围;
恒有意义,求实数a的取值范围; 上为增函数,并且
上为增函数,并且 .
. 时,画出函数
时,画出函数 的简图,并指出
的简图,并指出 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为 平方米,且高度不低于
平方米,且高度不低于 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段 与两腰长的和)为
与两腰长的和)为 (米).
(米).
 米,则其腰长
米,则其腰长 的定义域为
的定义域为  ,值域为
,值域为 ,则称函数
,则称函数 是
是 上的“四维方军”函数,求常数
上的“四维方军”函数,求常数 的值;
的值; 使函数
使函数 是区间
是区间 的值,否则,请说明理由.
的值,否则,请说明理由. 的奇函数
的奇函数 满足
满足 ,且当
,且当 时,
时,  .
. 上的解析式;
上的解析式; 取何值时,方程
取何值时,方程 在
在 上有解?
上有解?