题目内容
已知 是定义域为R的奇函数,
是定义域为R的奇函数, ,
,
⑴求实数 的值;
的值;
⑵若 在x∈[2,3]上恒成立,求
在x∈[2,3]上恒成立,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) 的取值范围是
的取值范围是 .
.
解析试题分析:(1)奇函数 中如果
中如果 时有意义,则必有
时有意义,则必有 ,这是我们解决这类问题的常用方法,当然也可用奇函数的定义来求解,
,这是我们解决这类问题的常用方法,当然也可用奇函数的定义来求解, ,
, ,化简得
,化简得 对于
对于 恒成立,则
恒成立,则 ;(2)本题不等式恒成立问题,我们是通过不等式知识把不等式变形为
;(2)本题不等式恒成立问题,我们是通过不等式知识把不等式变形为 ,即相当于分离参数法,因此
,即相当于分离参数法,因此 不大于
不大于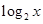 的最小值,从而问题转化为求
的最小值,从而问题转化为求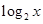 的最小值.
的最小值.
试题解析:解(1)∵ 是定义域为R的奇函数,
是定义域为R的奇函数,
∴ ,解得
,解得 .
.
(2)由(1) ,
,
不等式 为
为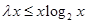 .
.
∵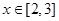 ,∴
,∴ .
.
在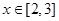 时,
时,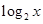 的最小值为
的最小值为 ,故
,故 ,
,
∴ 的取值范围是
的取值范围是 .
.
考点:1、奇函数的定义和性质;2、不等式恒成立问题.

练习册系列答案
相关题目
 且
且 ,函数
,函数 ,
, ,记
,记 .
. 的定义域
的定义域 及其零点;
及其零点; 的方程
的方程 在区间
在区间 内仅有一解,求实数
内仅有一解,求实数 的取值范围.
的取值范围. 是定义域为
是定义域为 的奇函数.
的奇函数. 的值;
的值; ,且
,且 在
在 上的最小值为
上的最小值为 ,求
,求 的值.
的值. 的图象分别与
的图象分别与 轴、
轴、 轴交于
轴交于 两点,且
两点,且 ,函数
,函数 ,当
,当 ,时,求函数
,时,求函数 的值域.
的值域. (
( ).
). 的单调区间;
的单调区间;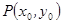 是曲线
是曲线 上的任意一点,若以
上的任意一点,若以 恒成立,求实数
恒成立,求实数 的最小值;
的最小值; 的方程
的方程 的实根情况.
的实根情况.  是定义在
是定义在 上的增函数,且
上的增函数,且
 的值;(2)、若
的值;(2)、若 ,解不等式
,解不等式 .
. 的一部分,栏栅与矩形区域的边界交于点
的一部分,栏栅与矩形区域的边界交于点 ,交曲线于点
,交曲线于点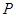 ,设
,设 .
.
 (
( 为坐标原点)的面积
为坐标原点)的面积 表示成
表示成 的函数
的函数 ;
; 处,
处, 的值及
的值及 :
: 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围; ,当
,当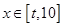 时,
时, 的值域为区间
的值域为区间 ,且
,且 .
. .
.
 成立的
成立的 的取值范围;
的取值范围; ,
, ,求实数
,求实数 的取值范围.
的取值范围.