题目内容
10.已知等边△ABC,边长为1,则|3$\overrightarrow{AB}$+4$\overrightarrow{BC}$|等于( )| A. | $\sqrt{37}$ | B. | 5 | C. | $\sqrt{13}$ | D. | 7 |
分析 根据已知条件可求出$\overrightarrow{AB}•\overrightarrow{BC}$=$-\frac{1}{2}$,所以根据$|3\overrightarrow{AB}+4\overrightarrow{BC}|=\sqrt{(3\overrightarrow{AB}+4\overrightarrow{BC})^{2}}$即可求得答案.
解答 解:|$3\overrightarrow{AB}+4\overrightarrow{BC}$|=$\sqrt{(3\overrightarrow{AB}{+4\overrightarrow{BC})}^{2}}$=$\sqrt{9+24×(-\frac{1}{2})+16}=\sqrt{13}$.
故选C.
点评 考查数量积的计算公式,注意正确求出向量的夹角,以及求向量$3\overrightarrow{AB}+4\overrightarrow{BC}$的长度的方法:$|3\overrightarrow{AB}+4\overrightarrow{BC}|=\sqrt{(3\overrightarrow{AB}+4\overrightarrow{AB})^{2}}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.给出演绎推理的“二段论”,已知函数f(x)=$\frac{1}{x}$在(-∞,0)∪(0,+∞)是单调递减的,有因为-1<2,所以f(-1)>f(2),即-1$>\frac{1}{2}$,这显然是不对的,那么这个推理是( )
| A. | 大前提推理 | B. | 小前提推理 | C. | 推理形式错误 | D. | 非以上错误 |
2.将5名同学分到甲、乙、丙三个小组,若甲组至少两人,乙、丙两组每组至少一人,则不同的分配方案共有( )种.
| A. | 80种 | B. | 120种 | C. | 140种 | D. | 50种 |
 “十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.
“十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.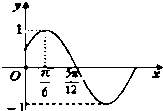 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,令${a_n}=f(\frac{nπ}{6})$,则a1+a2+a3+…+a2014=0.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,令${a_n}=f(\frac{nπ}{6})$,则a1+a2+a3+…+a2014=0.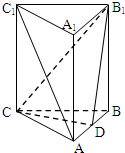 如图所示,在所有棱长都为2a的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,D点为棱AB的中点.
如图所示,在所有棱长都为2a的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,D点为棱AB的中点.