题目内容
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若存在区间
,若存在区间![]() 使得
使得![]() :
:
(Ⅰ)![]() 在
在![]() 上是单调函数;
上是单调函数;
(Ⅱ)![]() 在
在![]() 上的值域是
上的值域是![]() ,
,
则称区间![]() 为函数
为函数![]() 的“倍值区间”.
的“倍值区间”.
下列函数中存在“倍值区间”的有______________(填上所有你认为正确的序号)
①![]() ; ②
; ②![]() ;
;
③![]() ; ④
; ④![]() .
.
【答案】①②④
【解析】
函数中存在“倍值区间”,则![]() 在
在![]() 内是单调函数,
内是单调函数,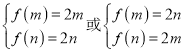 ,对四个函数的单调性分别研究,从而确定是否存在“倍值区间”.
,对四个函数的单调性分别研究,从而确定是否存在“倍值区间”.
函数中存在“倍值区间”,
则(Ⅰ)![]() 在
在![]() ,
,![]() 内是单调函数,(Ⅱ)
内是单调函数,(Ⅱ)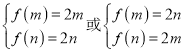 ,
,
对①,![]() ,若存在“倍值区间”
,若存在“倍值区间” ![]() ,则
,则![]()
![]()
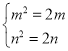
![]()
![]() ,
,![]() ,存在“倍值区间”
,存在“倍值区间” ![]() ;
;
对②,![]() ,若存在“倍值区间”
,若存在“倍值区间”![]() ,当
,当![]() 时,
时, ,故只需
,故只需![]() 即可,故存在;
即可,故存在;
对③,![]() ;当
;当![]() 时,在区间
时,在区间![]() ,
,![]() 上单调递减,在区间
上单调递减,在区间![]() ,
,![]() 上单调递增,
上单调递增,
若存在“倍值区间”![]() ,
,![]() ,
,
![]()
![]() 不符题意;
不符题意;
若存在“倍值区间”![]() ,
,![]() 不符题意,故此函数不存在“倍值区间“;
不符题意,故此函数不存在“倍值区间“;
对④,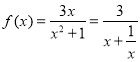 ,易得
,易得![]() 在区间
在区间![]() ,
,![]() 上单调递增,在区间
上单调递增,在区间![]() ,
,![]() 上单调递减,若存在“倍值区间”
上单调递减,若存在“倍值区间” ![]() ,
,![]() ,
,![]() ,即存在“倍值区间”
,即存在“倍值区间” ![]() ,
,![]() ;
;
故答案为:①②④.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目