题目内容
(2010•郑州三模)设集合A={(x,y)|x,y,1-x-y是三角形的三边长},则集合A所表示的平面区域的面积是
.
| 1 |
| 8 |
| 1 |
| 8 |
分析:先依据x,y,1-x-y是三角形的三边长,利用三角的两边之和大于第三边得到关于x,y的约束条件,再结合二元一次不等式(组)与平面区域的关系画出图形即可.
解答: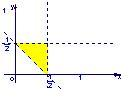 解:∵x,y,1-x-y是三角形的三边长,
解:∵x,y,1-x-y是三角形的三边长,
∴x>0,y>0,1-x-y>0,
并且x+y>1-x-y,x+(1-x-y)>y,y+(1-x-y)>x
∴
,
则集合A所表示的平面区域的面积是S=
×
×
=
故答案为:
.
 解:∵x,y,1-x-y是三角形的三边长,
解:∵x,y,1-x-y是三角形的三边长,∴x>0,y>0,1-x-y>0,
并且x+y>1-x-y,x+(1-x-y)>y,y+(1-x-y)>x
∴
|
则集合A所表示的平面区域的面积是S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.

练习册系列答案
相关题目