Question

（2010•郑州三模）从正方体的八个顶点中任取四个点连线，在能构成的一对异面直线中，其所成的角的度数不可能是（　　）

A．30°

B．45°

C．60°

D．90°

Answer 1

分析：根据正方体的8个顶点构成的异面直线中，先确定它们可能的大小，然后进行排除．

解答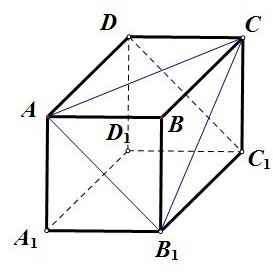：解：从正方体的八个顶点中任取四个点连线中，在能构成的一对异面直线中，其所成的角的度数可能有以下几种情况：
①若两异面直线为CD和A₁D₁，此时两直线所成的角为90°．．
②若两异面直线为CD和AB₁，此时两直线所成的角为45°．
③若两异面直线为AC和DC₁，此时两直线所成的角为60°．
所以在能构成的一对异面直线中，其所成的角的度数不可能是30°．
故选A．

点评：本题主要考查异面直线所成角的大小求法，比较基础．