题目内容
(本小题满分14分)
如图,椭圆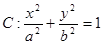
 的顶点为
的顶点为 焦点为
焦点为
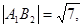 S□
S□ = 2S□
= 2S□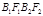 .
.

(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线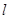 过P(1,1),且与椭圆相交于A,B两点,当P是AB的中点时,求直线
过P(1,1),且与椭圆相交于A,B两点,当P是AB的中点时,求直线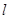 的方程.
的方程.
(Ⅲ)设n为过原点的直线,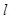 是与n垂直相交于P点、与
是与n垂直相交于P点、与
椭圆相交于A,B两点的直线, ,是否存在上述直线
,是否存在上述直线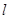 使以AB为直径的圆过原点?若存在,求出直线
使以AB为直径的圆过原点?若存在,求出直线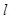 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
解:(1)由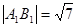 知
知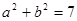 , ①
, ①
由S□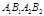 = 2S□
= 2S□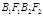 知
知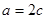 ,
②
,
②
又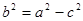 ,
③
,
③
由①,②,③解得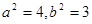 ,故椭圆C的方程为
,故椭圆C的方程为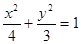 . …………4分
. …………4分
(Ⅱ)当直线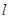 的斜率存在时,设直线
的斜率存在时,设直线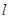 的方程为
的方程为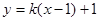 ,
,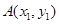 ,
,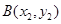 ,
,
则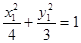 ,
,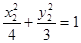 ,两式相减得:
,两式相减得: .
.
∵P是AB的中点,∴ 可得直线AB的斜率为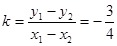 ,
,
∴直线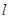 的方程为
的方程为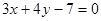 .
…………7分
.
…………7分
当直线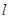 的斜率不存在时,将x=1代入椭圆方程并解得
的斜率不存在时,将x=1代入椭圆方程并解得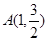 ,
,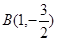 ,
,
这时AB的中点为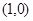 ,∴x=1不符合题设要求.
,∴x=1不符合题设要求.
综上,直线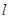 的方程为
的方程为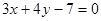 .
…………9分
.
…………9分
(Ⅲ)设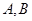 两点的坐标分别为
两点的坐标分别为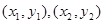 ,假设满足题设的直线
,假设满足题设的直线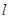 存在,
存在,
(i)当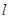 不垂直于
不垂直于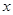 轴时,设
轴时,设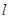 的方程为
的方程为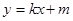 ,由
,由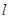 与
与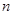 垂直相交于
垂直相交于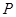 点且
点且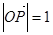 得
得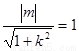 ,即
,即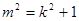 ,
,
又∵以AB为直径的圆过原点,∴OA⊥OB, ∴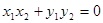 .
.
将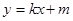 代入椭圆方程,得
代入椭圆方程,得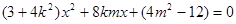 ,
,
由求根公式可得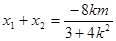 , ④
, ④
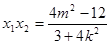 .
⑤
.
⑤
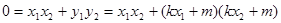
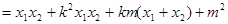
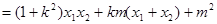 ,
,
将④,⑤代入上式并化简得
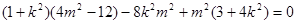 ,⑥
,⑥
将 代入⑥并化简得
代入⑥并化简得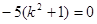 ,矛盾.
,矛盾.
即此时直线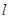 不存在.
…………12分
不存在.
…………12分
(ii)当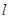 垂直于
垂直于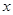 轴时,满足
轴时,满足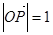 的直线
的直线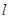 的方程为
的方程为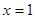 或
或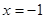 ,
,
当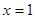 时,
时,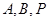 的坐标分别为
的坐标分别为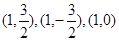 ,
,
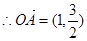 ,
,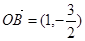 ,
,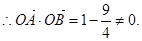
当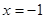 时,同理可得
时,同理可得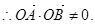
即此时直线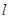 也不存在.
…………13分
也不存在.
…………13分
综上可知,使以AB为直径的圆过原点的直线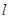 不存在. …………14分
不存在. …………14分
【解析】略

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)