题目内容
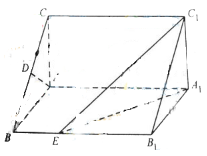
在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).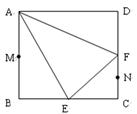
(Ⅰ)在三棱锥上标注出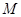 、
、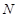 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;
(Ⅱ)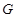 是线段
是线段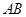 上一点,且
上一点,且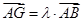 ,问是否存在点
,问是否存在点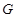 使得
使得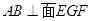 ,若存在,求出
,若存在,求出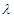 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)求多面体E-AFNM的体积.
(Ⅰ)参考解析;(Ⅱ)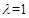 ;(Ⅲ)
;(Ⅲ)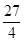
解析试题分析:(Ⅰ)通过翻折可知B点和C点对应的位置.所以可以相应地找到M,N点的位置.然后说明直线与平面AEF平行.
(Ⅱ)根据题意证得直线AB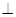 平面AEF.所以只需要动点G与点B重合即可得到AB
平面AEF.所以只需要动点G与点B重合即可得到AB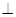 平面EGF.所以可得
平面EGF.所以可得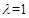 .本小题虽然是动点的问题但是通过证明线面垂直后再把动点移到特殊的位置即可.
.本小题虽然是动点的问题但是通过证明线面垂直后再把动点移到特殊的位置即可.
(Ⅲ)由于AB垂直于平面BEF,所以易计算三棱锥A-BEF的体积.同时四棱锥E-AFNM的体积与三棱锥E-BMN的体积比等于它们底面积的比.体积比转化为面积比的问题.从而可求出四棱锥E-AFMN的体积.本小题的体积求法有点技巧,要学会相互转化.
试题解析:(Ⅰ)因翻折后B、C、D重合,所以MN应是 的一条中位线,如图所示.
的一条中位线,如图所示.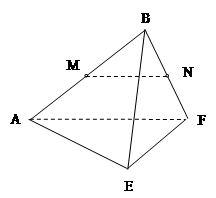
则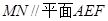 2分
2分
证明如下: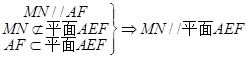 . 4分
. 4分
(Ⅱ)存在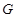 点使得
点使得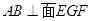 ,此时
,此时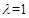
因为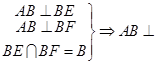 面EBF
面EBF
又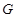 是线段
是线段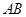 上一点,且
上一点,且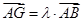 ,
,
∴当点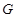 与点B重合时
与点B重合时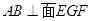 ,此时
,此时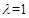 8分
8分
(Ⅲ)因为
且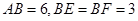 ,
,
∴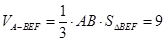 , 9分
, 9分
又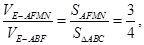
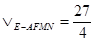 12分
12分
考点:1.图形的翻折.2.线面平行.3.线面垂直.4.四棱锥的体积.

练习册系列答案
相关题目
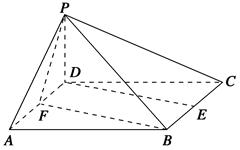
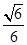 ,求四棱锥PABCD的体积.
,求四棱锥PABCD的体积.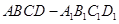 中,
中,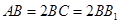 , 沿平面
, 沿平面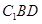 把这个长方体截成两个几何体: 几何体(1);几何体(2)
把这个长方体截成两个几何体: 几何体(1);几何体(2)
 、
、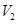 ,求
,求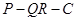 的正切值
的正切值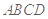 为矩形,
为矩形, 平面
平面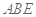 ,
,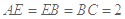 ,
,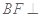 平面
平面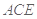 于点
于点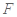 ,且点
,且点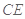 上.
上.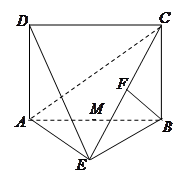
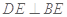 ;
;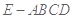 的体积;
的体积; 在线段
在线段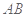 上,且
上,且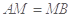 ,试在线段
,试在线段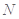 ,使得
,使得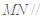 平面
平面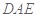 .
.
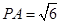 ,
,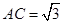 ,PB与底面ABC成60°角,
,PB与底面ABC成60°角,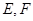 分别是
分别是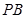 与
与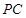 的中点,
的中点,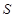 是线段
是线段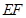 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体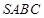 的体积。
的体积。
 为矩形,
为矩形, 平面
平面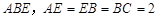 ,
,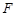 为
为 上的点,且
上的点,且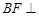 平面
平面 .
. 
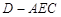 的体积;
的体积;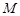 在线段
在线段 上,且满足
上,且满足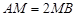 ,试在线段
,试在线段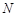 ,使得
,使得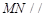 平面
平面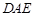 .
.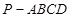 的底面是正方形,
的底面是正方形,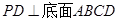 ,点
,点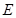 在棱
在棱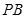 上.
上.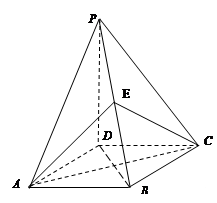
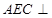 平面
平面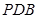 ;
;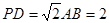 ,且
,且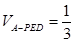 时,确定点
时,确定点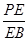 的值.
的值.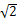 ,AA1=3,D是BC的中点,点E在菱BB1上运动。
,AA1=3,D是BC的中点,点E在菱BB1上运动。