题目内容
1.已知六棱柱 A BCD EF-A1 B1C1D1 E1F1的底面是正六边形,侧棱与底面垂直,若该六棱柱的侧面积为48,底面积为$12\sqrt{3}$,则该六棱柱外接球的表面积等于32π.分析 根据题意,利用六棱柱的侧面积为48,底面积为$12\sqrt{3}$,求出底面边长、侧棱长,利用勾股定理算出该六棱柱外接球的半径,再由球的表面积公式即可算出答案.
解答 解:设AB=a,AA1=b,则
∵六棱柱的侧面积为48,底面积为$12\sqrt{3}$,
∴6ab=48,$\frac{\sqrt{3}}{4}{a}^{2}•6•2$=12$\sqrt{3}$,
∴a=2,b=4,
∴该正六棱柱的外接球的半径R=$\sqrt{4+4}$=2$\sqrt{2}$.
∴该正六棱柱的外接球的表面积S=4πR2=32π.
故答案为:32π.
点评 本题给出六棱柱侧棱与底面垂直,六棱柱的侧面积为48,底面积为$12\sqrt{3}$,求它的外接球的表面积.考查几何体的表面积的求法,考查空间想象能力与计算能力.

练习册系列答案
相关题目
12.下列函数中,既是偶函数又在(-∞,0)上单调递增的是( )
| A. | y=x2 | B. | y=2|x| | C. | y=sin x | D. | y=log2$\frac{1}{|x|}$ |
13.函数f(x)=(x-1)ln|x|的图象大致为( )
| A. |  | B. | 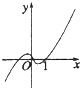 | C. | 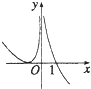 | D. |  |