题目内容
13.在四棱锥P-ABCD中,AB=AD=4,CD=BC=4,PA=4,AB⊥BC,PA⊥CD,平面PAB⊥平面ABCD.(1)证明:PC⊥BD;
(2)求直线PD与平面PBC所成角的正弦值.
分析 (1)转化为利用平面几何知识得出:BD⊥AC,利用直线平的垂直得出;BC⊥平面PAB,PA⊥BC,PA⊥BD,BD⊥面PAC,最后再转换为线线垂直得出PC⊥BD;
(2)建立坐标系求出=(6,2,-4),=(-2,2,0),=(0,4,-4),
设平面PBC的法向量为=(x1,y1,z1),利用$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=0}\\{\overrightarrow{n}\overrightarrow{BC}=0}\end{array}\right.$,求解得出=(3,6),令与=(3,6),夹角为α,直线PD与平面PBC所成角为θ,
利用数量积得出sinθ=|cosα|.
解答 证明:(1)底面ABCD的图形中:AB=AD=4,CD=BC=4,AB⊥BC,
利用平面几何知识得出:BD=4,AC=8,BD⊥AC,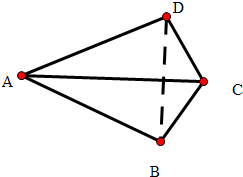
∵AB⊥BC,BC?平面ABCD,
平面PAB∩平面ABCD,
平面PAB⊥平面ABCD,
∴BC⊥平面PAB,
∵PA?平面PAB,
∴PA⊥BC,
∵PA⊥CD,BC∩CD=C,
∴PA⊥面ABCD,
又∵BD?面ABCD,
∴PA⊥BD,
又∵BD⊥AC,PA∩AC=A,
∴BD⊥面PAC,
∵PC?面PAC,
∴PC⊥BD;
(2)建立坐标系如图;A(0,0,0),P(0,0,4),D(0,4,0),B(6,2,0),C(4,4,0),
∴=(6,2,-4),=(-2,2,0),=(0,4,-4),
设平面PBC的法向量为=(x1,y1,z1),
∵$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=0}\\{\overrightarrow{n}\overrightarrow{BC}=0}\end{array}\right.$
∴$\left\{\begin{array}{l}{6{x}_{1}+2\sqrt{3}{y}_{1}-4{z}_{1}=0}\\{-2{x}_{1}+2\sqrt{3}{y}_{1}=0}\end{array}\right.$
求解得出=(3,6),
∵与=(3,6),夹角为α,直线PD与平面PBC所成角为θ
则cosα=$\frac{4\sqrt{3}×\sqrt{3}-4×6}{\sqrt{16+48}×\sqrt{9+3+36}}$=-,
∴直线PD与平面PBC所成角的正弦值sinθ=|cosα|=
点评 本题考查了空间直线平面的垂直问题,关键是确定直线与直线的垂直,直线与平面的垂直,面面的垂直,求解夹角问题可以转化为向量的运算,再结合法向量求解,属于计算较麻烦的题目,做题仔细认真.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
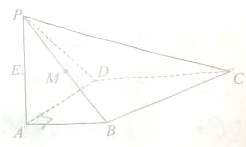 如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点.
如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点.