题目内容
8.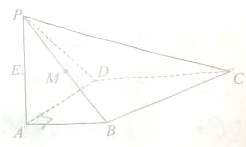 如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点.
如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点.(1)试在CD上确定一点N,使得MN∥平面PAD;
(2)点N在满足(1)的条件下,求直线MN与平面PAB所成角的正弦值.
分析 (1)CN=$\frac{1}{3}$ND,MN∥平面PAD,过M作ME∥AB交PA于E,连接DE,证明MN∥DE即可;
(2)利用MN∥DE,考的直线MN与平面PAB所成角等于直线DE与平面PAB所成角.解△AED即可.
解答 (1)证明:CN=$\frac{1}{3}$ND,MN∥平面PAD.
过M作ME∥AB交PA于E,连接DE.
∵CN=$\frac{1}{3}$ND,
∴CN=$\frac{1}{4}$CD=$\frac{1}{2}$AB=EM.
又EM∥DC∥AB,∴EM∥DN,且EM=DN
∴DEMN为平行四边形,
∴MN∥DE,
又DE?平面PAD,MN?平面PAD,
∴MN∥平面PAD.
(2)解:∵MN∥DE
∴直线MN与平面PAB所成角等于直线DE与平面PAB所成角
∵PA⊥底面ABCD,
∴PA⊥AD,
∵AB⊥AD,PA∩AB=A,
∴AD⊥平面PAB,
∴∠AED为直线DE与平面PAB所成角.
∵AE=$\frac{1}{2}$,AD=1,
∴DE=$\frac{\sqrt{5}}{2}$,
∴sin∠AED=$\frac{1}{\frac{\sqrt{5}}{2}}$=$\frac{2\sqrt{5}}{5}$.
∴直线MN与平面PAB所成角的正弦值为$\frac{2\sqrt{5}}{5}$.
点评 本题考查线面平行,线面角,考查学生分析解决问题的能力,正确运用线面平行的判定是关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
16.若m,n是互不相同的空间直线,α,β是不重合的平面,则下列命题中为假命题的是( )
| A. | 若m∥α,m?β,α∩β=nα∩β=n则m∥n | |
| B. | 若m⊥α,n⊥α,则m∥n | |
| C. | 若m?α,n?α,m∥β,n∥β,m∩n=O,m∩n=O,则α∥β | |
| D. | 若α⊥β,m?α,则m⊥β |
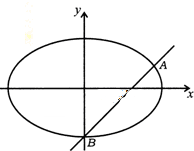 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的下顶点为B,右焦点为F,直线BF与椭圆E的另一个交点为A,$\overrightarrow{BF}=3\overrightarrow{FA}$.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的下顶点为B,右焦点为F,直线BF与椭圆E的另一个交点为A,$\overrightarrow{BF}=3\overrightarrow{FA}$.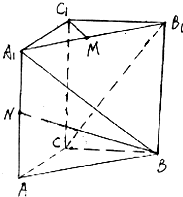 如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=2,AB=2$\sqrt{2}$,棱AA1=4,M,N分别是A1B1,AA1的中点.
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=2,AB=2$\sqrt{2}$,棱AA1=4,M,N分别是A1B1,AA1的中点.