题目内容
17.设复数z=a+bi,a,b∈R,z(2+3i)=-1+5i,则复数z=1+i.分析 把已知的等式变形,然后利用复数代数形式的乘除运算化简求值.
解答 解:由z=a+bi,a,b∈R,且z(2+3i)=-1+5i,
得$z=\frac{-1+5i}{2+3i}=\frac{(-1+5i)(2-3i)}{(2+3i)(2-3i)}$=$\frac{-2+3i+10i+15}{13}=1+i$.
故答案为:1+i.
点评 本题考查了复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
2.已知sin2α=a,cos2α=b,则tan(α+$\frac{π}{4}$)=( )
| A. | $\frac{a}{1+b}$ | B. | $\frac{1+a}{b}$ | C. | $\frac{1+a+b}{1-a+b}$ | D. | $\frac{a-b+1}{a+b-1}$ |
9.集合A={α|α=k•$\frac{π}{2}$-$\frac{π}{6}$,k∈Z},B={β|-π<β<π},则A∩B=( )
| A. | {-$\frac{2π}{3}$,$\frac{π}{3}$} | B. | {-$\frac{2π}{3}$,$\frac{5π}{6}$} | C. | {-$\frac{2π}{3}$,-$\frac{π}{6}$,$\frac{π}{3}$,$\frac{5π}{6}$} | D. | {-$\frac{2π}{3}$,$\frac{π}{3}$} |
6. 已知某空间几何体的三视图如图所示,其体积V为定值2$\sqrt{5}$,AB=AC,AD⊥BC,AD=$\sqrt{5}$,则m+n的最小值为( )
已知某空间几何体的三视图如图所示,其体积V为定值2$\sqrt{5}$,AB=AC,AD⊥BC,AD=$\sqrt{5}$,则m+n的最小值为( )
 已知某空间几何体的三视图如图所示,其体积V为定值2$\sqrt{5}$,AB=AC,AD⊥BC,AD=$\sqrt{5}$,则m+n的最小值为( )
已知某空间几何体的三视图如图所示,其体积V为定值2$\sqrt{5}$,AB=AC,AD⊥BC,AD=$\sqrt{5}$,则m+n的最小值为( )| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{3}$ |
 .
.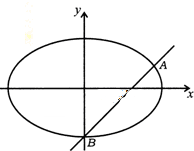 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的下顶点为B,右焦点为F,直线BF与椭圆E的另一个交点为A,$\overrightarrow{BF}=3\overrightarrow{FA}$.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的下顶点为B,右焦点为F,直线BF与椭圆E的另一个交点为A,$\overrightarrow{BF}=3\overrightarrow{FA}$.