题目内容
【题目】已知p:“x0∈(-1,1),x-x0-m=0(m∈R)”是正确的,设实数m的取值集合为M.
(1)求集合M;
(2)设关于x的不等式(x-a)(x+a-2)<0(a∈R)的解集为N,若“x∈M”是“x∈N”的充分条件,求实数a的取值范围.
【答案】(1) M={m|-![]() ≤m<2};(2){a|a>
≤m<2};(2){a|a>![]() 或a<-
或a<-![]() }.
}.
【解析】试题分析:(1)若命题![]() 为真命题,利用参数分类法结合一元二次函数的性质求出
为真命题,利用参数分类法结合一元二次函数的性质求出![]() 的范围即可求集合
的范围即可求集合![]() ;(2)若
;(2)若![]() 是
是![]() 的充分条件,则
的充分条件,则![]() ,分类讨论当
,分类讨论当![]() 即
即![]() 时,
时, ![]() ,当
,当![]() 即
即![]() 时,
时, ![]() ,当
,当![]() 即
即![]() 时,
时, ![]() 三种情况进行求.
三种情况进行求.
试题解析:(1)由题意知,方程![]() 在
在![]() 上有解,
上有解,
故![]() 的取值集合就是函数
的取值集合就是函数![]() 在
在![]() 上的值域,易得
上的值域,易得![]() .
.
(2)因为“![]() ”是“
”是“![]() ”的充分条件,所以
”的充分条件,所以![]() .
.
当![]() 时,集合
时,集合![]() 为空集,不满足题意;当
为空集,不满足题意;当![]() 时,
时, ![]() ,此时集合
,此时集合![]() ,则
,则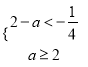 ,解得
,解得![]() ;
;
当![]() 时,
时, ![]() ,此时集合
,此时集合![]() ,则
,则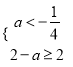 解得
解得![]() ,综上可知,实数
,综上可知,实数![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.

练习册系列答案
相关题目