题目内容
【题目】共享单车是指企业的校园，地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务，是一种分时租赁模式，某共享单车企业为更好服务社会，随机调查了100人，统计了这100人每日平均骑行共享单车的时间（单位：分钟），由统计数据得到如下频率分布直方图，已知骑行时间在
三组对应的人数依次成等差数列
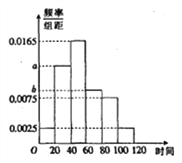
（1）求频率分布直方图中
的值.
（2）若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”，将日平均骑行时间少于40分钟的用户为“潜力用户”，现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人，再从这5人中任取3人，求恰好1人为“忠实用户”的概率.
【答案】(1) 
， 
;(2) 
.
【解析】试题分析：（1）根据直方图各矩形面积和为
可得
，从而可得
的值，在根据
三组对应的人数依次成等差数列求出
的值；（2）列举出这
人中任选
人共
种情形，符合题设条件有共有
种，根据古典概型概率公式可得恰好
人为“忠实用户”的概率.
试题解析：（1）由
，
又
，所以
.
（2）“忠实用户”“潜力用户”的人数之比为： 
，
所以“忠实用户”抽取
人，“潜力用户”抽取
人，
记事件：从
人中任取
人恰有
人为“忠实用户”
设两名“忠实用户”的人记为： 
，三名“潜力用户”的人记为： 
，
则这5人中任选3人有： 
，共10种情形，
符合题设条件有： 
共有6种，因此概率为
.
练习册系列答案
字词句段篇系列答案
相关题目
