题目内容
16.已知x≥1,y≥0,集合A={(x,y)|x+y≤4},B={(x,y)|x-y+t=0},如果A∩B≠∅,则t的取值范围是[-4,2]..分析 把A∩B≠∅转化为线性规划问题,作出可行域,由直线x-y+t=0与可行域有交点求得t的范围.
解答 解:由$\left\{\begin{array}{l}{x≥1}\\{y≥0}\\{x+y≤4}\end{array}\right.$作出可行域如图,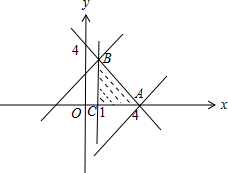
要使A∩B≠∅,则直线x-y+t=0与可行域有公共点,
联立$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$,得B(1,3),
又A(4,0),
把A,B的坐标分别代入直线x-y+t=0,得t=-4,t=2.
∴-4≤t≤2.
故答案为:[-4,2].
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
4.“a>b”是“3a>3b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.设a=sin393°,b=cos55°,c=tan50°,则a,b,c的大小关系为( )
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | a<c<b |
16.已知△ABC的面积为1,三边长分别为a,b,c,则a2+2bc的最小值为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
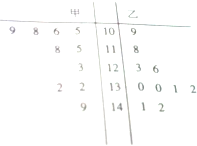 如图记录了甲、乙两名同学其中10次数学成绩.
如图记录了甲、乙两名同学其中10次数学成绩. 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,PC=AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,PC=AB=2AD=2CD=2,E是PB的中点.