题目内容
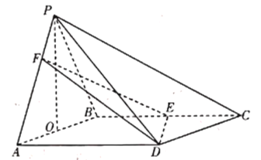
【题目】已知椭圆的中心为坐标原点O,椭圆短半轴长为1,动点![]()
![]() 在直线
在直线![]() ,(
,(![]() 为长半轴,
为长半轴,![]() 为半焦距)上.
为半焦距)上.
(1)求椭圆的标准方程
(2)求以OM为直径且被直线![]() 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N.求证:线段ON的长为定值,并求出这个定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析,定值为
;(3)证明见解析,定值为![]()
【解析】
(1)由题可知![]() ,
,![]() ,再结合
,再结合![]() ,可求出
,可求出 ![]() ,从而可得椭圆的标准方程;
,从而可得椭圆的标准方程;
(2)设出以OM为直径的圆的方程,变为标准方程后找出圆心和半径,由以OM为直径的圆被直线![]() 截得的弦长为2,过圆心作弦的垂线,根据垂径定理得到垂足为中点,由弦的一半,半径以及圆心到直线的距离即弦心距构成直角三角形,利用点到直线的距离公式表示出圆心到直线
截得的弦长为2,过圆心作弦的垂线,根据垂径定理得到垂足为中点,由弦的一半,半径以及圆心到直线的距离即弦心距构成直角三角形,利用点到直线的距离公式表示出圆心到直线![]() 的距离
的距离![]() ,根据勾股定理列出关于
,根据勾股定理列出关于![]() 的方程,求出方程的解即可得到的值,即可确定出所求圆的方程;
的方程,求出方程的解即可得到的值,即可确定出所求圆的方程;
(3)设出点![]() 的坐标,表示出
的坐标,表示出![]() 及
及![]() ,由
,由![]() ,得到两向量的数量积为0,利用平面向量的数量积的运算法则表示出一个关系式,又
,得到两向量的数量积为0,利用平面向量的数量积的运算法则表示出一个关系式,又![]() ,同理根据平面向量的数量积的运算法则得到另一个关系式,把前面得到的关系式代入,即可求出线段ON的长,从而得到线段ON的长为定值.
,同理根据平面向量的数量积的运算法则得到另一个关系式,把前面得到的关系式代入,即可求出线段ON的长,从而得到线段ON的长为定值.
(1)又由点M在准线上,得![]()
故![]() ,
,![]()
从而![]()
所以椭圆方程为![]()
(2)以OM为直径的圆的方程为![]()
即![]()
其圆心为![]() ,半径
,半径![]()
因为以OM为直径的圆被直线![]() 截得的弦长为2
截得的弦长为2
所以圆心到直线![]() 的距离
的距离![]()
![]()
所以![]() ,
,
解得![]()
所求圆的方程为![]()
(3)方法一:由平面几何知:![]()
直线OM:![]() ,直线FN:
,直线FN:![]()
由 得
得![]()

所以线段ON的长为定值![]() .
.
方法二、设![]() ,则
,则 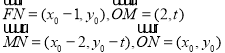
![]()
又![]()
所以,![]() 为定值
为定值

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目