题目内容
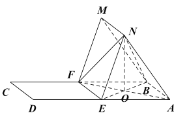
【题目】如图，平行四边形ABCD中，
，E、F分别为AD，BC的中点．以EF为折痕把四边形EFCD折起，使点C到达点M的位置，点D到达点N的位置，且
．
（1）求证：
平面NEB；
（2）若
，求二面角
的余弦值．
【答案】（1）见解析（2）
．
【解析】
（1）记
，连接NO，证明
即可证明结论；
（2）先证明
平面ABFE，再以直线OE为x轴，直线OA为y轴，直线ON为
轴建立空间直角坐标系，求出平面MBE的法向量
，平面NBE的一个法向量
，代入向量的夹角公式，即可求得二面角
的余弦值．
（1）证明：记，连接NO，
可知四边形ABFE是菱形，所以
，且O为AF，BE的中点，
又
，所以
，
又因为
，NO，
平面NEB，
所以
平面NEB.
（2）因为
，所以
，
，
所以
，
所以
，
所以
，所以
，
又由（1）可知：
，且，AF，平面ABFE，
所以平面ABFE，以直线OE为x轴，直线OA为y轴，直线ON为轴建立空间直角坐标系，
则
，
，
，
，
，
所以
，所以
，
，
设
是平面MBE的法向量，则
，取
，得，
又平面NBE的一个法向量为，
所以
，
所以二面角的余弦值为．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
