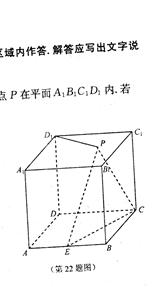
题目内容
若实数x,y满足
+
=10,则t=
+
的最大值为______.
| x2+(y+3)2 |
| x2+(y-3)2 |
| x |
| 4 |
| y |
| 5 |
由实数x,y满足
+
=10,
由题意的定义可知:点P(x,y)在以(0,±3)为焦点,10为长轴长的椭圆
+
=1上.
可设
,
∴t=
+
=cosθ+sinθ=
(
cosθ+
sinθ)=
sin(θ+
)≤
.当且仅当sin(θ+
)=1时取等号.
故答案为
.
| x2+(y+3)2 |
| x2+(y-3)2 |
由题意的定义可知:点P(x,y)在以(0,±3)为焦点,10为长轴长的椭圆
| y2 |
| 25 |
| x2 |
| 16 |
可设
|
∴t=
| x |
| 4 |
| y |
| 5 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
故答案为
| 2 |

练习册系列答案
相关题目
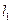 的参数方程为
的参数方程为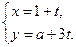 (
(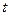 为参数),直线
为参数),直线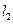 的方程为
的方程为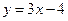 ,若直线
,若直线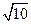 ,则实数
,则实数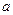 的值为 .
的值为 .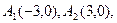
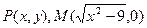 ,若实数
,若实数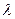 使向量
使向量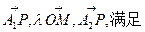
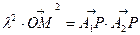 。
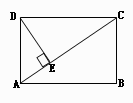
。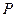 的轨迹方程,并判断
的轨迹方程,并判断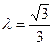 时,过点
时,过点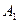 且斜率为
且斜率为 的直线与此时(1)中的曲线相交的另一点为
的直线与此时(1)中的曲线相交的另一点为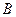 ,能否在直线
,能否在直线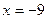 上找一点
上找一点 ,使
,使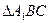 为正三角形(请说明理由)。
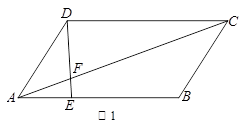
为正三角形(请说明理由)。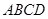 中,点
中,点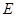 在
在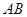 上且
上且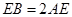 ,
,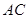 与
与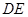 交于点
交于点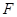 ,则
,则 .
.
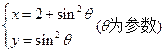 化为普通方程为( )
化为普通方程为( )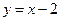
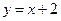
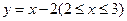
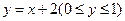
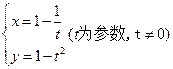 ,则它的普通方程为__________________。
,则它的普通方程为__________________。