题目内容
(本小题满分12分)(原创题)
在平面直角坐标系中,已知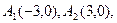
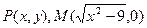 ,若实数
,若实数 使向量
使向量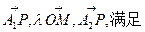
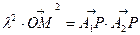 。
。
(1)求点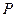 的轨迹方程,并判断
的轨迹方程,并判断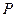 点的轨迹是怎样的曲线;
点的轨迹是怎样的曲线;
(2)当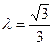 时,过点
时,过点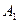 且斜率为
且斜率为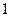 的直线与此时(1)中的曲线相交的另一点为
的直线与此时(1)中的曲线相交的另一点为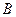 ,能否在直线
,能否在直线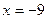 上找一点
上找一点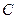 ,使
,使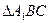 为正三角形(请说明理由)。
为正三角形(请说明理由)。
在平面直角坐标系中,已知
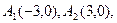
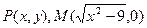 ,若实数
,若实数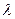 使向量
使向量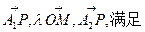
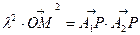 。
。(1)求点
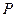 的轨迹方程,并判断
的轨迹方程,并判断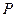 点的轨迹是怎样的曲线;
点的轨迹是怎样的曲线;(2)当
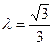 时,过点
时,过点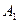 且斜率为
且斜率为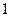 的直线与此时(1)中的曲线相交的另一点为
的直线与此时(1)中的曲线相交的另一点为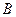 ,能否在直线
,能否在直线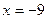 上找一点
上找一点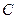 ,使
,使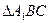 为正三角形(请说明理由)。
为正三角形(请说明理由)。当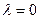 时,方程为
时,方程为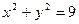 ,P的轨迹是圆。
,P的轨迹是圆。
当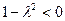 ,即
,即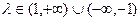 时,方程为
时,方程为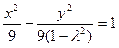 ,
,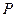 点的轨迹是双曲线。
点的轨迹是双曲线。
当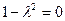 ,即
,即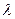 =±1时,方程为
=±1时,方程为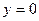 ,
,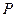 点的轨迹是射线。,在直线
点的轨迹是射线。,在直线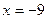 上找不到点
上找不到点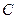 满足条件
满足条件
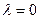 时,方程为
时,方程为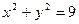 ,P的轨迹是圆。
,P的轨迹是圆。当
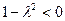 ,即
,即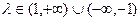 时,方程为
时,方程为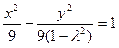 ,
,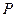 点的轨迹是双曲线。
点的轨迹是双曲线。当
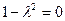 ,即
,即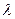 =±1时,方程为
=±1时,方程为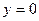 ,
,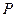 点的轨迹是射线。,在直线
点的轨迹是射线。,在直线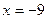 上找不到点
上找不到点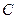 满足条件
满足条件解:(1)由已知可得,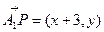 ,
,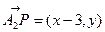 ,
,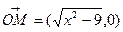 ,
,
∵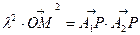 ,∴
,∴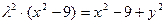
即 点的轨迹方程
点的轨迹方程
当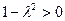 ,且
,且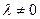 ,即
,即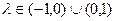 时,有
时,有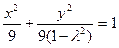 ,
,
∵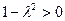 ,∴
,∴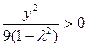 ,∴
,∴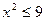
∴P点的轨迹是点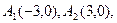 为长轴的焦点在
为长轴的焦点在 轴上的椭圆。………………………………3分
轴上的椭圆。………………………………3分
当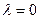 时,方程为
时,方程为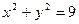 ,P的轨迹是圆。
,P的轨迹是圆。
当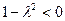 ,即
,即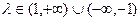 时,方程为
时,方程为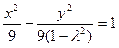 ,
,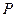 点的轨迹是双曲线。
点的轨迹是双曲线。
当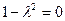 ,即
,即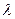 =±1时,方程为
=±1时,方程为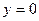 ,
,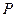 点的轨迹是射线。……………………6分
点的轨迹是射线。……………………6分
(2)过点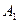 且斜率为
且斜率为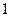 的直线方程为
的直线方程为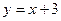 ,
,
当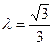 时,曲线方程为
时,曲线方程为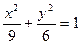 ,
,
由(1)知,其轨迹为以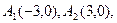 为长轴的焦点在
为长轴的焦点在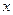 轴上的椭圆。
轴上的椭圆。
因直线过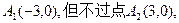
所以,点B不存在。
所以,在直线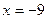 上找不到点
上找不到点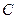 满足条件。 …………………………12分
满足条件。 …………………………12分
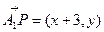 ,
,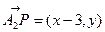 ,
,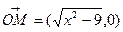 ,
,∵
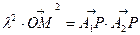 ,∴
,∴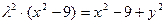
即
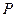 点的轨迹方程
点的轨迹方程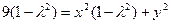
当
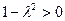 ,且
,且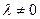 ,即
,即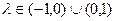 时,有
时,有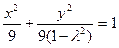 ,
,∵
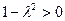 ,∴
,∴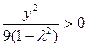 ,∴
,∴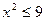
∴P点的轨迹是点
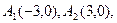 为长轴的焦点在
为长轴的焦点在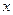 轴上的椭圆。………………………………3分
轴上的椭圆。………………………………3分当
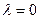 时,方程为
时,方程为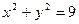 ,P的轨迹是圆。
,P的轨迹是圆。当
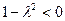 ,即
,即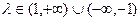 时,方程为
时,方程为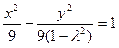 ,
,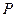 点的轨迹是双曲线。
点的轨迹是双曲线。当
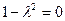 ,即
,即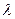 =±1时,方程为
=±1时,方程为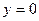 ,
,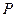 点的轨迹是射线。……………………6分
点的轨迹是射线。……………………6分(2)过点
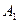 且斜率为
且斜率为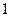 的直线方程为
的直线方程为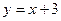 ,
,当
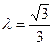 时,曲线方程为
时,曲线方程为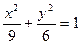 ,
,由(1)知,其轨迹为以
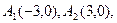 为长轴的焦点在
为长轴的焦点在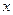 轴上的椭圆。
轴上的椭圆。因直线过
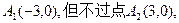
所以,点B不存在。
所以,在直线
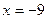 上找不到点
上找不到点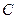 满足条件。 …………………………12分
满足条件。 …………………………12分
练习册系列答案
相关题目
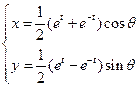 化为普通方程:
化为普通方程: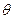 为参数,
为参数,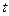 为常数;(2)
为常数;(2)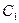 :
: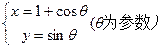 上的点到曲线
上的点到曲线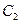 :
: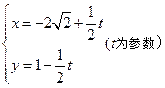 上的点的最短距离为 .
上的点的最短距离为 .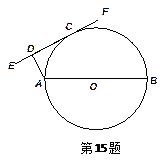
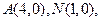 若点
若点 满足
满足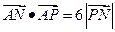 。
。 的取值范围;
的取值范围;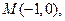 求
求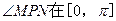 上的取值范围。
上的取值范围。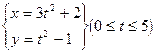
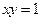 化为以
化为以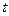 参数的参数方程是( )
参数的参数方程是( )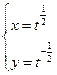

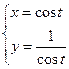
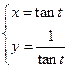
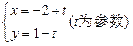 被圆
被圆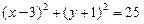 所截得的弦长为 .
所截得的弦长为 .