题目内容
【题目】在数列{an}中，已知a1=1，a2=2，an+2= 
（k∈N*）．
（1）求数列{an}的通项公式；
（2）求满足2an+1=an+an+2的正整数n的值；
（3）设数列{an}的前n项和为Sn ， 问是否存在正整数m，n，使得S2n=mS2n﹣1？若存在，求出所有的正整数对（m，n）；若不存在，请说明理由．
【答案】
（1）解：由a1=1，a2=2，an+2= 
（k∈N*）．可得数列{an}的奇数项是以1为首项，公差为2的等差数列；偶数项是以2为首项，公比为3的等比数列．
∴对任意正整数k，a2k﹣1=1+2（k﹣1）=2k﹣1；a2k=2×3k﹣1．
∴数列{an}的通项公式a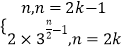n= 
，k∈N*
（2）解：①当n为奇数时，由2an+1=an+an+2可得： 
=n+n+2，化为： 
=n+1，
令f（x）=2× 
﹣x﹣1（x≥1），
由f′（x）= 
× 
×ln 
﹣1≥ 
﹣1=ln3﹣1＞0，
可知f（x）在[1，+∞）上是增函数，
∴f（x）≥f（1）=0，
∴当且仅当n=1时，满足 
=n+1，即2a2=a1+a3．
②当n为偶数时，由2an+1=an+an+2可得：2（n+1）=2 +2× 
，
化为：n+1= 
+ 
，
上式左边为奇数，右边为偶数，因此不成立．
综上，满足2an+1=an+an+2的正整数n的值只有1
（3）解：S2n=（a1+a3+…+a2n﹣1）+（a2+a4+…+a2n）= 
+ 
=3n+n2﹣1，n∈N*．
S2n﹣1=S2n﹣a2n=3n﹣1+n2﹣1．
假设存在正整数m，n，使得S2n=mS2n﹣1，
则3n+n2﹣1=m（3n﹣1+n2﹣1），
∴3n﹣1（3﹣m）=（m﹣1）（n2﹣1），（*）
从而3﹣m≥0，∴m≤3，
又m∈N*，∴m=1，2，3．
①当m=1时，（*）式左边大于0，右边等于0，不成立．
②当m=3时，（*）式左边等于0，∴2（n2﹣1）=0，解得n=1，∴S2=3S1．
③当m=2时，（*）式可化为3n﹣1=（n+1）（n﹣1），
则存在k1，k2∈N*，k1＜k2，使得n﹣1= 
，n+1= 
，且k1+k2=n﹣1，
从而 
= 
=2，∴ ﹣ =2， =1，
∴k1=0，k2﹣k1=1，于是n=2，S4=2S3．
综上可知，符合条件的正整数对（m，n）只有两对：（2，2），（3，1）
【解析】（1）由题意可得数列{an}的奇数项是以1为首项，公差为2的等差数列；偶数项是以2为首项，公比为3的等比数列．分别利用等差数列与等比数列的通项公式即可得出．（2）①当n为奇数时，由2an+1=an+an+2可得： =n+n+2，化为： =n+1，令f（x）=2× ﹣x﹣1（x≥1），利用导数研究函数的单调性即可得出．②当n为偶数时，由2an+1=an+an+2可得：2（n+1）=2 +2× 
，化为：n+1= + ，即可判断出不成立．（3）S2n=（a1+a3+…+a2n﹣1）+（a2+a4+…+a2n）=3n+n2﹣1，n∈N* ． S2n﹣1=S2n﹣a2n=3n﹣1+n2﹣1．假设存在正整数m，n，使得S2n=mS2n﹣1 ， 化为3n﹣1（3﹣m）=（m﹣1）（n2﹣1），可得1，2，3．分类讨论即可得出．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系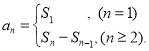
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
