题目内容
设数列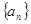 的前
的前 项积为
项积为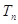 ,且
,且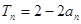
 .
.
(Ⅰ)求证数列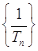 是等差数列;
是等差数列;
(Ⅱ)设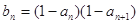 ,求数列
,求数列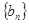 的前
的前 项和
项和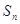 .
.
(Ⅰ)只需证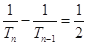 即可;(Ⅱ)
即可;(Ⅱ)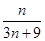 。
。
解析试题分析:(Ⅰ)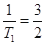 1分
1分
由题意可得: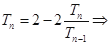
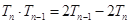
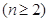 ,
,
所以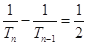 6分
6分
(Ⅱ)数列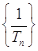 为等差数列,
为等差数列,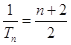 ,
,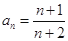 , 8分
, 8分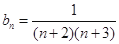 10分
10分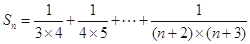
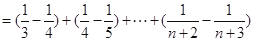
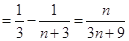 12分
12分
考点:等差数列的性质;数列通项公式的求法;数列前n项和的求法;裂项法。
点评:常见的裂项公式: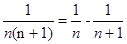 ,
,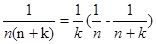 ,
,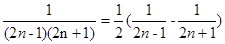 ,
,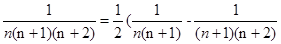 ,
, ,
,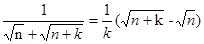 。
。

练习册系列答案
相关题目
题目内容
设数列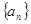 的前
的前 项积为
项积为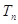 ,且
,且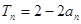
 .
.
(Ⅰ)求证数列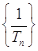 是等差数列;
是等差数列;
(Ⅱ)设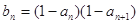 ,求数列
,求数列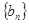 的前
的前 项和
项和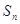 .
.
(Ⅰ)只需证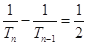 即可;(Ⅱ)
即可;(Ⅱ)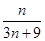 。
。
解析试题分析:(Ⅰ)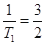 1分
1分
由题意可得: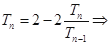
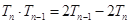
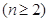 ,
,
所以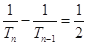 6分
6分
(Ⅱ)数列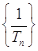 为等差数列,
为等差数列,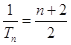 ,
,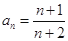 , 8分
, 8分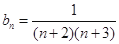 10分
10分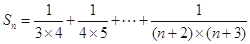
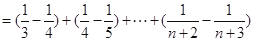
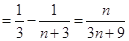 12分
12分
考点:等差数列的性质;数列通项公式的求法;数列前n项和的求法;裂项法。
点评:常见的裂项公式: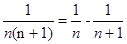 ,
,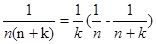 ,
,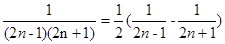 ,
,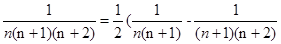 ,
, ,
,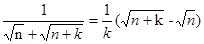 。
。
