题目内容
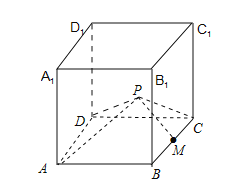
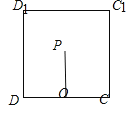
【题目】已知棱长为3的正方体ABCD﹣A1B1C1D1中,M是BC的中点,点P是侧面DCC1D1内(包括边界)的一个动点,且满足∠APD=∠MPC.则当三棱锥P﹣BCD的体积最大时,三棱锥P﹣BCD的外接球的表面积为_____.
【答案】21π
【解析】
由题意得三角形相似,再借助函数求最大值,求出![]() 的位置在棱
的位置在棱![]() 上,且
上,且![]() 时三棱锥的体积最大,然后由三棱锥为一条侧棱垂直于底面的三棱锥,它的外接球的球心是过底面外接圆的圆心做垂直于底面的直线与中截面的交点,而底面为直角三角形,所以底面外接圆的圆心为斜边的中点,且半径为斜边的一半,根据底面外接圆的半径与球的半径和三棱锥的高的一半构成直角三角形,由题意求出外接球的半径,求出外接球的表面积.
时三棱锥的体积最大,然后由三棱锥为一条侧棱垂直于底面的三棱锥,它的外接球的球心是过底面外接圆的圆心做垂直于底面的直线与中截面的交点,而底面为直角三角形,所以底面外接圆的圆心为斜边的中点,且半径为斜边的一半,根据底面外接圆的半径与球的半径和三棱锥的高的一半构成直角三角形,由题意求出外接球的半径,求出外接球的表面积.
由题意得![]() 是
是![]() 的中点,点
的中点,点![]() 是侧面
是侧面![]() 内(包括边界)的一个动点,
内(包括边界)的一个动点,
且满足![]()
![]() ,
,![]()
![]() ,及
,及![]() .
.
设![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
化简得![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 点在
点在![]() 上,且
上,且![]() 时三棱锥
时三棱锥![]() 的体积最大,
的体积最大,
这时底面外接圆圆心为斜边![]() 的中点
的中点![]() ,球心为过
,球心为过![]() 垂直于底面的直线与中截面的交点
垂直于底面的直线与中截面的交点![]() ,
,
则![]() ,底面半径
,底面半径![]() ,设球的半径
,设球的半径![]() ,则,
,则,![]() ,
,
所以三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某绿色有机水果店中一款有机草莓味道鲜甜,店家每天以每斤![]() 元的价格从农场购进适量草莓,然后以每斤
元的价格从农场购进适量草莓,然后以每斤![]() 元的价格出售,如果当天卖不完,剩下的草莓由果汁厂以每斤
元的价格出售,如果当天卖不完,剩下的草莓由果汁厂以每斤![]() 元的价格回收.
元的价格回收.
(1)若水果店一天购进![]() 斤草莓,求当天的利润
斤草莓,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:斤,
(单位:斤,![]() )的函数解析式;
)的函数解析式;
(2)水果店记录了![]() 天草莓的日需求量(单位:斤),整理得下表:
天草莓的日需求量(单位:斤),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 14 | 22 | 14 | 16 | 15 | 13 | 6 |
①假设水果店在这![]() 天内每天购进
天内每天购进![]() 斤草莓,求这
斤草莓,求这![]() 天的日利润(单位:元)的平均数;
天的日利润(单位:元)的平均数;
②若水果店一天购进![]() 斤草莓,以
斤草莓,以![]() 天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于
天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于![]() 元的概率.
元的概率.