题目内容
【题目】已知椭圆
（
），以椭圆内一点
为中点作弦
，设线段
的中垂线与椭圆相交于
， 
两点．
（Ⅰ）求椭圆的离心率；
（Ⅱ）试判断是否存在这样的
，使得
， 
， 
， 
在同一个圆上，并说明理由．
【答案】（Ⅰ）
（Ⅱ）存在这样的
，使得
， 
， 
， 
在同一个圆上．
【解析】【试题分析】（1）借助递椭圆离心率的定义分析求解；（2）依据题设条件先建立直线的方程，再与椭圆方程联立，借助交点坐标之间的关系分析求解：
（Ⅰ）将椭圆方程化成标准方程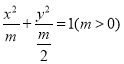
， 
．
（Ⅱ）由题意，设
， 
， 
， 
，直线
的斜率存在，设
为
，联立
，
得
．
， 
，此时由
，得
，
则
： 
， 
： 
．
则
得
， 
，故
的中点
为
．
由弦长公式可得到
．
，若存在圆，则圆心在
上，
的中点
到直线
的距离为
．
，
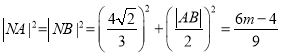又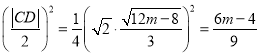
存在这样的
，使得
， 
， 
， 
在同一个圆上．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
