题目内容
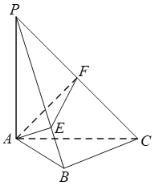
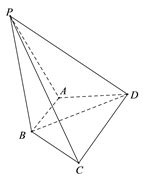
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ∥
∥![]() ,且
,且![]()
![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)证明见解析;(Ⅱ)![]() .
.
【解析】试题分析:(1)证明面面垂直,一般利用面面垂直判定定理,即从线面垂直进行论证,而线面垂直证明,往往需要多次利用线线垂直与线面垂直的转化,而线线垂直,有时可利用平几条件进行寻找与论证,如本题取![]() 中点E,利用平几知识得到四边形
中点E,利用平几知识得到四边形![]() 是矩形,从而得到
是矩形,从而得到![]() ,而易得
,而易得![]() ,因此
,因此![]() ,进而有平面
,进而有平面![]() 平面
平面![]() ;(2)利用空间向量求线面角,首先建立空间直角坐标系:以A 为原点,
;(2)利用空间向量求线面角,首先建立空间直角坐标系:以A 为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标角系,设出各点坐标,利用方程组解出面的法向量,利用向量数量积求夹角,最后根据线面角与向量夹角互余得结论
轴,建立空间直角坐标角系,设出各点坐标,利用方程组解出面的法向量,利用向量数量积求夹角,最后根据线面角与向量夹角互余得结论
试题解析:解:证明:(1)![]() 为
为![]() 中点,
中点, ![]() ,
, ![]() ,且
,且![]() 四边形
四边形![]() 是矩形,
是矩形, ![]() ,又
,又![]() 平面
平面![]() ,且
,且![]() ,
,![]() 在平面
在平面![]() 中,
中, ![]() 平面
平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
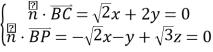
(2)以A 为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标角系,
轴,建立空间直角坐标角系,
![]() ,
,
![]() 则
则![]()
![]()
设平面![]() 的法向量
的法向量![]() ,则
,则 ,取
,取![]() ,得
,得 ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,  ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】某消费品企业销售部对去年各销售地的居民年收入(即此地所有居民在一年内的收入的总和)及其产品销售额进行抽样分析,收集数据整理如下:
销售地 | A | B | C | D |
年收入x(亿元) | 15 | 20 | 35 | 50 |
销售额y(万元) | 16 | 20 | 40 | 48 |
(1)在图a中作出这些数据的散点图,并指出y与x成正相关还是负相关?
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程?
(3)若B地今年的居民年收入将增长20%,预测B地今年的销售额将达到多少万元?
回归方程系数公式: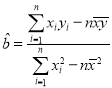 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【题目】某校夏令营有3名男同学![]() 和3名女同学
和3名女同学![]() ,其年级情况如下表:
,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
用表中字母列举出所有可能的结果
设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件![]() 发生的概率.
发生的概率.