题目内容
已知二次函数f(x)=x2+2bx+c(b、c∈R).
(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b、c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,求实数b的取值范围.
(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b、c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,求实数b的取值范围.
(1)b=0,c=-1
(2) <b<
<b<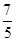
(2)
 <b<
<b<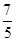
解:(1)依题意,x1=-1,x2=1是方程x2+2bx+c=0的两个根.
由韦达定理,得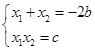 即
即
所以b=0,c=-1.
(2)由题知,f(1)=1+2b+c=0,所以c=-1-2b.
记g(x)=f(x)+x+b=x2+(2b+1)x+b+c=x2+(2b+1)x-b-1,
则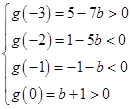 ,
,
解得 <b<
<b<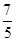 ,
,
所以实数b的取值范围为 <b<
<b<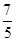 .
.
由韦达定理,得
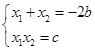 即
即
所以b=0,c=-1.
(2)由题知,f(1)=1+2b+c=0,所以c=-1-2b.
记g(x)=f(x)+x+b=x2+(2b+1)x+b+c=x2+(2b+1)x-b-1,
则
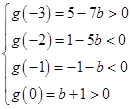 ,
,解得
 <b<
<b<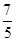 ,
,所以实数b的取值范围为
 <b<
<b<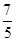 .
.
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
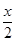 +
+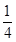 .
.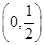 ,使f(x0)=x0.
,使f(x0)=x0.
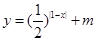 的图像与
的图像与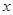 轴有公共点,则
轴有公共点,则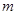 的取值范围是_______.
的取值范围是_______.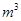 ,高为
,高为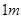 的无盖长方形容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是_______(单位:元)
的无盖长方形容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是_______(单位:元)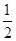 <x≤m+
<x≤m+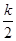 (k∈Z)对称.其中正确命题的序号是________.
(k∈Z)对称.其中正确命题的序号是________.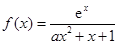 ,其中
,其中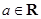 .
.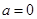 ,求函数
,求函数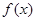 的定义域和极值;
的定义域和极值;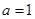 时,试确定函数
时,试确定函数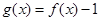 的零点个数,并证明.
的零点个数,并证明.