Question

【题目】如图，为圆上的动点，定点，线段的垂直平分线交线段于点．

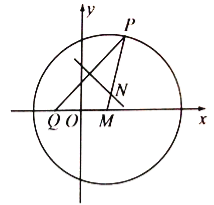
（1）求动点的轨迹方程；

（2）记动点的轨迹为曲线 ，设圆的切线交曲线于两点，求的最大值．

Answer 1

【答案】（1）；（2）

【解析】

试题分析：（1）考虑到点在线段的垂直平分线上，因此有是常数，从椭圆定义知，其轨迹是椭圆，由椭圆标准方程可得轨迹方程；（2）当切线垂直坐标轴时，求得，在切线不垂直坐标轴时，设切线的方程：，同时点，由直线和圆相切，得，把代入椭圆方程，可得，然后计算，但直接计算不方便，通过计算，得，由直角三角形的面积可得，由弦长公式计算出，并把代入得关于的函数，设后可求得其最大值．

试题解析：（1）因为，

所以动点的轨迹为椭圆，

∴，∴，

∴动点的轨迹方程为；

（2）①当切线垂直坐标轴时，；

②当切线不垂直坐标轴时，设切线的方程：，点，由直线和圆相切，得

由得，，

∴

∴

，

∴，∴

又∵，

令，则，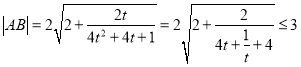

当且仅当时，等号成立，

∴，

综上，的最大值为