题目内容
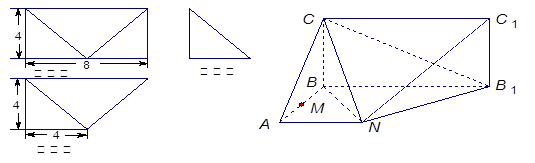
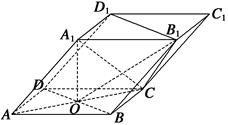
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B = 900,D为棱BB1上一点,且面DA1 C⊥面AA1C1C.求证:D为棱BB1中点;(2)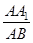 为何值时,二面角A -A1D - C的平面角为600.
为何值时,二面角A -A1D - C的平面角为600.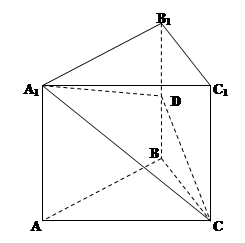
(1)见解析;(2)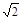 .
.
解析试题分析:(1)过点D作DE ⊥ A1 C 于E点,取AC的中点F,连BF ﹑EF,先证直线DE⊥面AA1C1C,再证BF⊥面AA1C1C,得D,E,F,B共面,再证DB∥EF ,从而有EF∥AA1,易得所证结论;(2)法1:建立空间直角坐标系,找出所需点的坐标,分别设出面DA1C和平面AA1DB的法向量,并列方程计算出来,再利用向量的数量积计算两向量的夹角的余弦值,便可得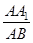 得值;法2:延长A1 D与直线AB相交于G,易知CB⊥面AA1B1B,过B作BH⊥A1 G于点H,连CH,证明∠CHB为二面角A -A1D - C的平面角,在
得值;法2:延长A1 D与直线AB相交于G,易知CB⊥面AA1B1B,过B作BH⊥A1 G于点H,连CH,证明∠CHB为二面角A -A1D - C的平面角,在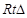 CHB中,根据条件计算
CHB中,根据条件计算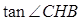 的表达式,可得结论.
的表达式,可得结论.
试题解析:(1)过点D作DE ⊥ A1 C 于E点,取AC的中点F,连BF ﹑EF.
∵面DA1 C⊥面AA1C1C且相交于A1 C,面DA1 C内的直线DE ⊥ A1 C,∴直线DE⊥面AA1C1C ,3分
又∵面BA C⊥面AA1C1C且相交于AC,易知BF⊥AC,∴BF⊥面AA1C1C
由此知:DE∥BF ,从而有D,E,F,B共面,又易知BB1∥面AA1C1C,故有DB∥EF ,从而有EF∥AA1,
又点F是AC的中点,所以DB = EF = 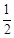 AA1=
AA1= 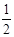 BB1,所以D点为棱BB1的中点; 6分
BB1,所以D点为棱BB1的中点; 6分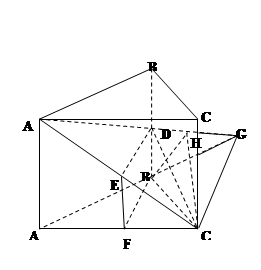
(2)解法1:建立如图所示的直角坐标系,设AA1= 2b ,AB=BC = ,则D(0,0,b), A1 (a,0,2b), C (0,a,0), 7分
,则D(0,0,b), A1 (a,0,2b), C (0,a,0), 7分
所以,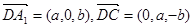 , 8分
, 8分
设面DA1C的法向量为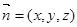 则
则  可取
可取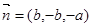 ,
,
又可取平面AA1DB的法向量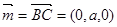 ,
,
cos〈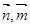 〉
〉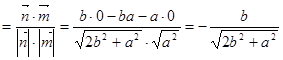 , 10分
, 10分
据题意有: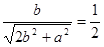 , 12分
, 12分
解得: 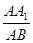 =
=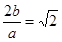 . 13分
. 13分
解法2:延长A1 D与直线AB相交于G,易知CB⊥面AA1B1B,
过B作BH⊥A1 G于点H,连CH,由三垂线定理知:A1 G⊥CH,
由此知∠CHB为二面角A -A1D - C的平面角; 9分
设AA1= 2b ,AB=BC = ;在直角三角形A1A G中,易知AB = BG.
;在直角三角形A1A G中,易知AB = BG.
在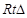 DBG中,BH =
DBG中,BH = 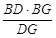 =
= 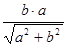 , 10分
, 10分
在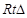 CHB中,tan∠CHB =
CHB中,tan∠CHB = 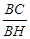 =
= 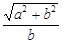 ,
,
据题意有: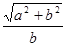 = tan600 =
= tan600 = 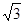 ,
,
解得: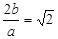 所以
所以 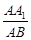 =
=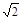 . 13分
. 13分
考点:1、面面垂直的性质;2、二面角;3、利用空间向量解决几何问题.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案、过点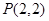 的直线与圆
的直线与圆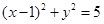 相切,且与直线
相切,且与直线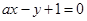 垂直,则
垂直,则 ( ).
( ).
A.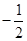 | B.1 | C.2 | D. |
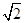 .
.
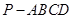 中,
中, ⊥平面
⊥平面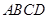 ,底面
,底面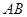 ∥
∥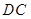 ,
,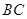 ,
,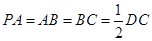 ,点
,点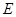 在棱
在棱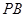 上,且
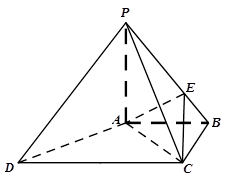
上,且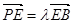 .
.
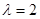 时,求证:
时,求证: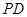 ∥面
∥面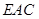 ;
;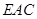 所成角为
所成角为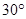 ,求实数
,求实数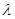 的值.
的值.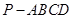 中,
中,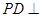 底面
底面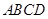 ,底面
,底面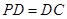 ,
,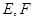 分别是
分别是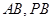 的中点.
的中点.
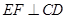 ;
; 内求一点
内求一点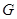 ,使
,使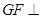 平面
平面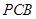 ,并证明你的结论;
,并证明你的结论;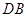 与平面
与平面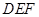 所成角的正弦值.
所成角的正弦值.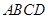 -
-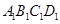 中,
中,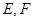 分别为
分别为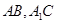 的中点. 应用空间向量方法求解下列问题.
的中点. 应用空间向量方法求解下列问题. 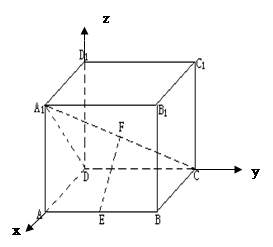
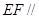 平面
平面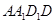 ;
;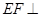 平面
平面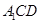 .
.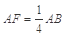 .
.
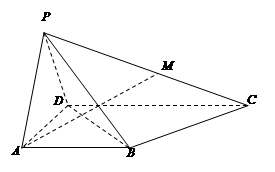
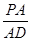 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?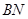 ⊥平面
⊥平面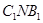 (2)求平面
(2)求平面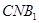 与平面
与平面