题目内容
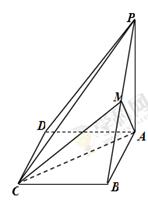
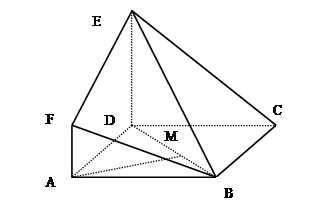
如图,在四棱锥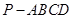 中,
中,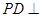 底面
底面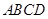 ,底面
,底面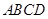 为正方形,
为正方形,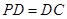 ,
,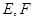 分别是
分别是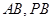 的中点.
的中点.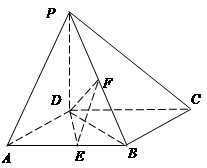
(1)求证: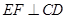 ;
;
(2)在平面 内求一点
内求一点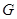 ,使
,使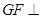 平面
平面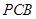 ,并证明你的结论;
,并证明你的结论;
(3)求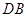 与平面
与平面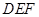 所成角的正弦值.
所成角的正弦值.
(1)详见解析;(2)详见解析;(3)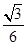
解析试题分析:在空间中直线、平面的平行和垂直关系的判定,求空间中的角,可以用相关定义和定理解决,如(1)中,易证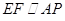 ,
,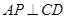 ,所以,
,所以,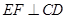 ,但有些位置关系很难转化,特别求空间中的角,很难找到直线在平面内的射影,很难作出二面角,这时空间向量便可大显身手,如果图形便于建立空间直角坐标系,则更为方便,本题就是建立空间直角坐标系,写出各点坐标(1)计算
,但有些位置关系很难转化,特别求空间中的角,很难找到直线在平面内的射影,很难作出二面角,这时空间向量便可大显身手,如果图形便于建立空间直角坐标系,则更为方便,本题就是建立空间直角坐标系,写出各点坐标(1)计算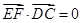 即可;(2)设
即可;(2)设 ,再由
,再由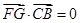 ,
, 解出
解出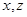 ,即可找出点
,即可找出点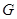 ;(3)用待定系数法求出件可求出平面
;(3)用待定系数法求出件可求出平面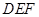 的法向量,再求出平面
的法向量,再求出平面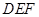 的法向量与向量平面
的法向量与向量平面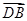 的夹角的余弦,从而得到结果.
的夹角的余弦,从而得到结果.
试题解析:以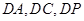 所在直线为
所在直线为 轴、
轴、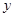 轴、
轴、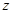 轴建立空间直角坐标系(如图),设
轴建立空间直角坐标系(如图),设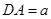 ,则
,则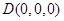 ,
,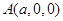 ,
,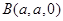 ,
, ,
,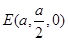 ,
,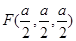 ,
,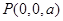 .
.
(1)因为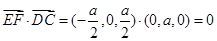 ,所以
,所以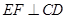 . 4分
. 4分
(2)设 ,则
,则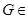 平面
平面 ,
,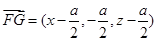 ,
,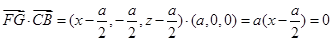 ,所以
,所以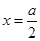 ,
,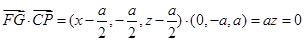 ,所以
,所以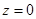
∴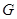 点坐标为
点坐标为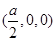 ,即
,即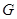 点为
点为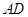 的中点. 8分
的中点. 8分
(3)设平面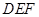 的法向量为
的法向量为 .
.
由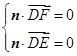 得,
得,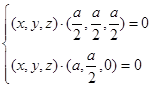 即
即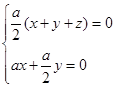 ,
,
取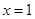 ,则
,则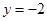 ,
,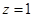 ,得
,得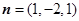 .
.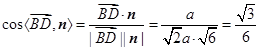 ,
,
所以,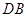 与平面
与平面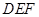 所成角的正弦值的大小为
所成角的正弦值的大小为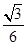 13分
13分
考点:空间向量与立体几何.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
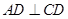 ,
,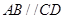 ,
,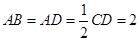 ,点M在线段EC上(除端点外)
,点M在线段EC上(除端点外)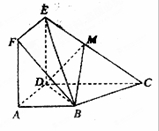
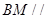 平面
平面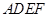 ;
;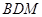 与平面ABF所成二面角为锐角,且该二面角的余弦值为
与平面ABF所成二面角为锐角,且该二面角的余弦值为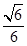 时,求三棱锥
时,求三棱锥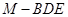 的体积
的体积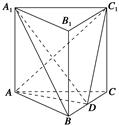
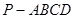 中,
中,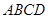 为平行四边形,且
为平行四边形,且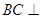 平面
平面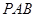 ,
,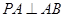 ,
,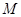 为
为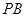 的中点,
的中点,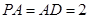 .
.
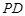 //
//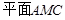 ;
;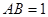 , 求二面角
, 求二面角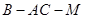 的余弦值.
的余弦值. 是边长为3的正方形,
是边长为3的正方形, ,
,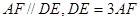 ,
,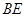 与平面
与平面 .
.
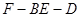 的的余弦值;
的的余弦值;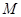 是线段
是线段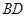 上一动点,试确定
上一动点,试确定 ,并证明你的结论.
,并证明你的结论. 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直,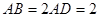 ,点
,点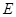 为
为 的中点.
的中点.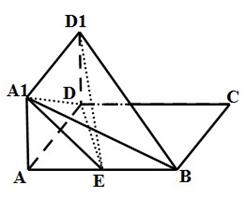
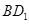 ∥平面
∥平面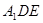 ;
;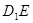
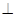
 ;
;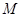 ,使二面角
,使二面角 的大小为
的大小为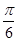 ?若存在,求出
?若存在,求出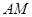 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.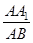 为何值时,二面角A -A1D - C的平面角为600.
为何值时,二面角A -A1D - C的平面角为600.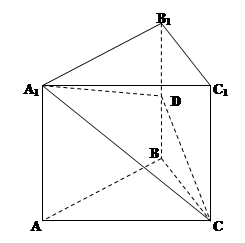
 为正三角形,
为正三角形,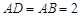 ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为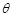 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在
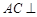 平面PBD;
平面PBD;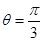 时,求二面角
时,求二面角 的余弦值。
的余弦值。 是PC的中点,设
是PC的中点,设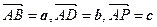 .
.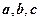 表示出向量
表示出向量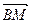 ;
; 的长.
的长.