题目内容
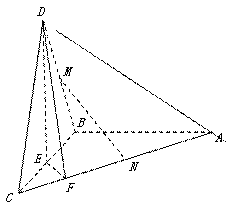
已知:四棱锥P—ABCD的底面为直角梯形,且AB∥CD,∠DAB=90o,DC=2AD=2AB,侧面PAD与底面垂直,PA=PD,点M为侧棱PC上一点.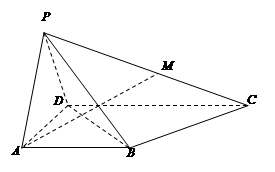
(1)若PA=AD,求PB与平面PAD的所成角大小;
(2)问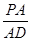 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?
(1)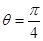
(2)AM⊥平面PDB不可能成立.
解析试题分析:解:(1)以AD中点O为坐标原点,建立如图所示空间直角坐标系,设AB=2
则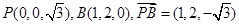 2分
2分
平面PAD的法向量就是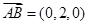
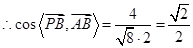 4分
4分
设所求夹角为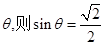 ,则
,则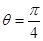 5分
5分
(2)设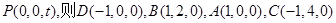
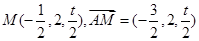 ,
,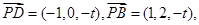 7分
7分
若AM⊥平面PDB,则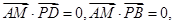 8分
8分
得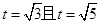 不可能同时成立,AM⊥平面PDB不可能成立. 10分
不可能同时成立,AM⊥平面PDB不可能成立. 10分
考点:空间中垂直问题以及线面角
点评:主要是考查了线面角的求解,以及线面垂直的证明,属于中档题。

练习册系列答案
相关题目
直线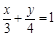 与两坐标轴围成的三角形的周长为( )
与两坐标轴围成的三角形的周长为( )
A.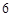 | B.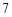 | C. | D.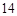 |
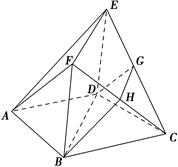
 是边长为3的正方形,
是边长为3的正方形, ,
,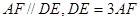 ,
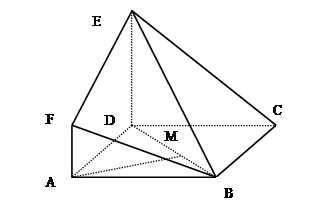
,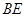 与平面
与平面 .
.
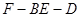 的的余弦值;
的的余弦值;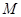 是线段
是线段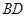 上一动点,试确定
上一动点,试确定 ,并证明你的结论.
,并证明你的结论.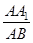 为何值时,二面角A -A1D - C的平面角为600.
为何值时,二面角A -A1D - C的平面角为600.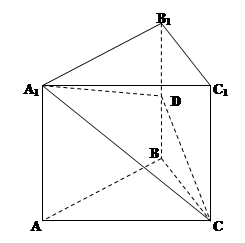
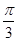 ,D、E分别为AA1、A1C的中点.
,D、E分别为AA1、A1C的中点.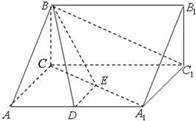
 为正三角形,
为正三角形,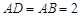 ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为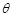 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在
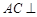 平面PBD;
平面PBD;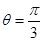 时,求二面角
时,求二面角 的余弦值。
的余弦值。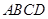 中,
中,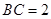 ,
, ,
,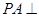 平面
平面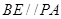 ,
,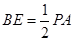 ,
,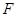 为
为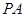 的中点.
的中点.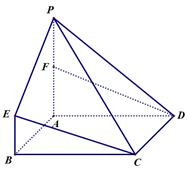
 平面
平面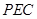 .
.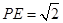 ,求平面
,求平面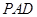 所成锐二面角的余弦值.
所成锐二面角的余弦值.