题目内容
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且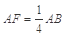 .
.
(Ⅰ)求证:EF∥平面BDC1;
(Ⅱ)求二面角E-BC1-D的余弦值.
(1)要证明线面平行,则先证明EF∥A1O,然后利用下面平行的判定定理来得到。
(2)
解析试题分析:(1)证法一:设O为AB的中点,连结A1O,
∵AF=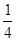 AB ,O为AB的中点
AB ,O为AB的中点
∴F为AO的中点,又E为AA1的中点
∴EF∥A1O
又∵D为A1B1的中点,O为AB的中点
∴A1D=OB 又A1D∥OB
∴四边形A1DBO为平行四边形
∴A1O∥BD 又EF∥A1O ∴EF∥BD
又EF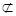 平面DBC1, BD
平面DBC1, BD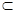 平面DBC1 ∴EF∥平面DBC1 (6分)
平面DBC1 ∴EF∥平面DBC1 (6分)
证法二:建立如图所示的坐标系。(坐标系建立仅为参考)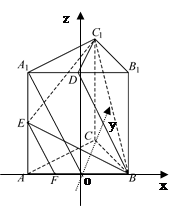
∵AB=BC=CA=AA1=2,D、E分别为A1B1、AA1的中点,AF=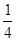 AB
AB
E(-1,0,1),F ,B(1,0,0),D(0,0,2),C1(0,
,B(1,0,0),D(0,0,2),C1(0,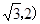 )
)
设平面平面DBC1的法向量为
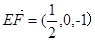 ,
, ,
,
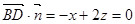
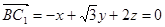
令z=1,则y=0,x=2 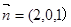

∴  又EF
又EF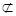 平面BDC1 ∴EF∥平面BDC1 (6分)
平面BDC1 ∴EF∥平面BDC1 (6分)
(2)设面EBC1的法向量为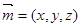
 ,
,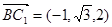
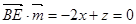

令x=1,则z=2,y=- ∴
∴ 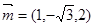
cos< >=
>=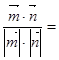

由图知二面角E-BC1-D为锐二面角,所以二面角的余弦值为 (12分)
(12分)
考点:线面平行,和二面角的平面角
点评:主要是考查了熟练的根据几何性质来证明平行性质,以及运用空间向量法求解角,属于中档题。

练习册系列答案
相关题目
已知直线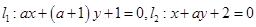 ,则“
,则“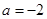 ”是“
”是“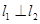 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |

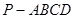 中,
中,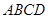 为平行四边形,且
为平行四边形,且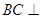 平面
平面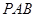 ,
,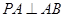 ,
,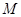 为
为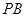 的中点,
的中点,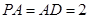 .
.
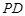 //
//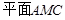 ;
;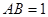 , 求二面角
, 求二面角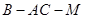 的余弦值.
的余弦值.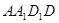 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直,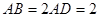 ,点
,点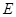 为
为 的中点.
的中点.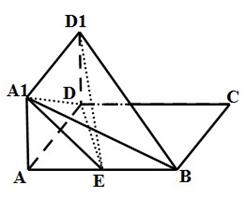
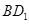 ∥平面
∥平面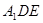 ;
;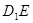
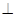
 ;
;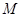 ,使二面角
,使二面角 的大小为
的大小为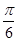 ?若存在,求出
?若存在,求出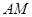 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.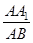 为何值时,二面角A -A1D - C的平面角为600.
为何值时,二面角A -A1D - C的平面角为600.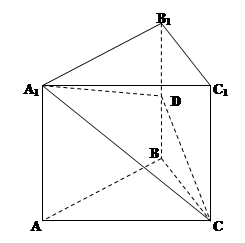
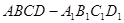 的棱长为
的棱长为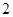 ,
,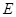 、
、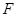 分别是
分别是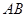 、
、 的中点.
的中点.
 的体积;
的体积;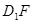 与平面
与平面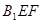 所成角的余弦值.
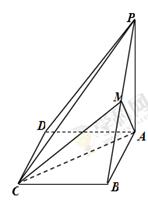
所成角的余弦值.  为正三角形,
为正三角形,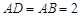 ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为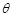 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在
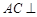 平面PBD;
平面PBD;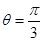 时,求二面角
时,求二面角 的余弦值。
的余弦值。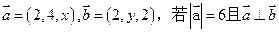 ,求
,求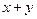 的值.
的值.